Advanced

Lecture 0. Introduction

抢一个做展示的Project，占20分 + 一个不做展示的 Bonus

Omega 时间复杂度下限 / O 时间复杂度上限

Lecture 1. AVL Trees, Splay Trees, and Amortized Analysis

AVL Trees

二叉搜索树：左子树比根小，右子树比根大 - 要使得它更可能平衡。

AVL: $T$ is Height Balanced：左子树 与 右子树 的 差 的绝对值 $\leq 1$。

Balance Factor (BF) = $h_L - h_R$，平衡树中应为 $-1, 0, \text{or } 1$。

siblings：兄弟姐妹。

Rotations

RR Rotation: Trouble Maker (刚进入的节点) in the RR (Right subtree's Right subtree) of Trouble Finder (发现不平衡的第一个节点)

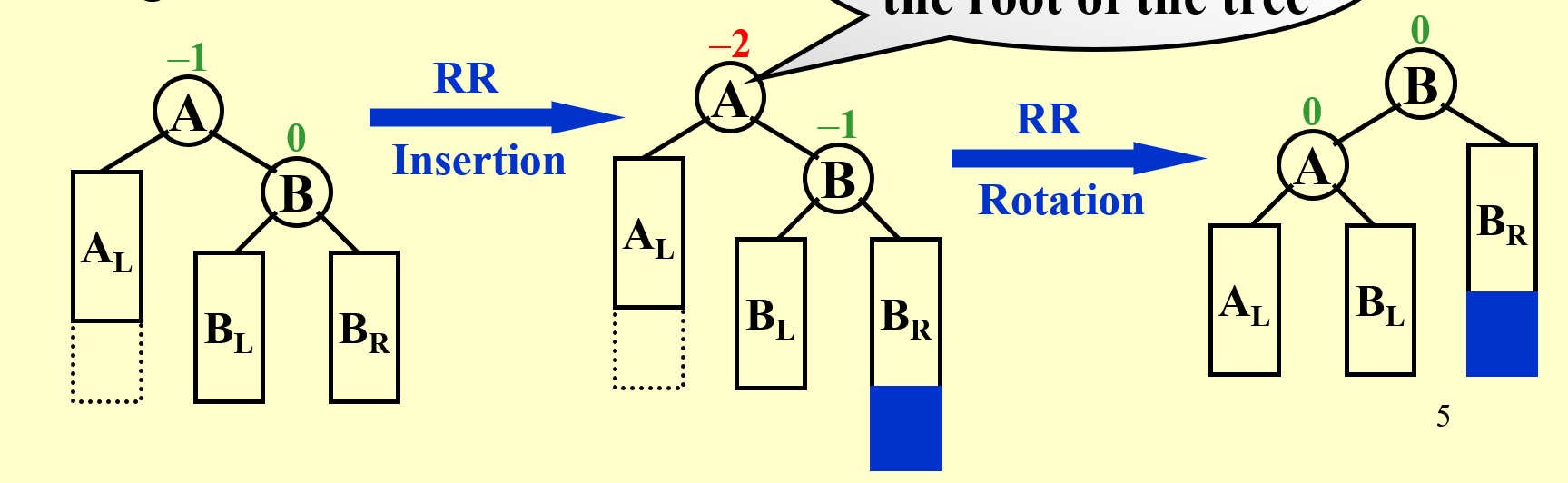
把 B 的左子树连到 A 的右子树上，把 A 作为 B 的左子树。要记得更新这一坨与他们的父亲之间的联系，即把 A 原来的父亲变成 B 的父亲。

LL Rotation: 类似地，Trouble Maker 是 Trouble Finder 的 LL

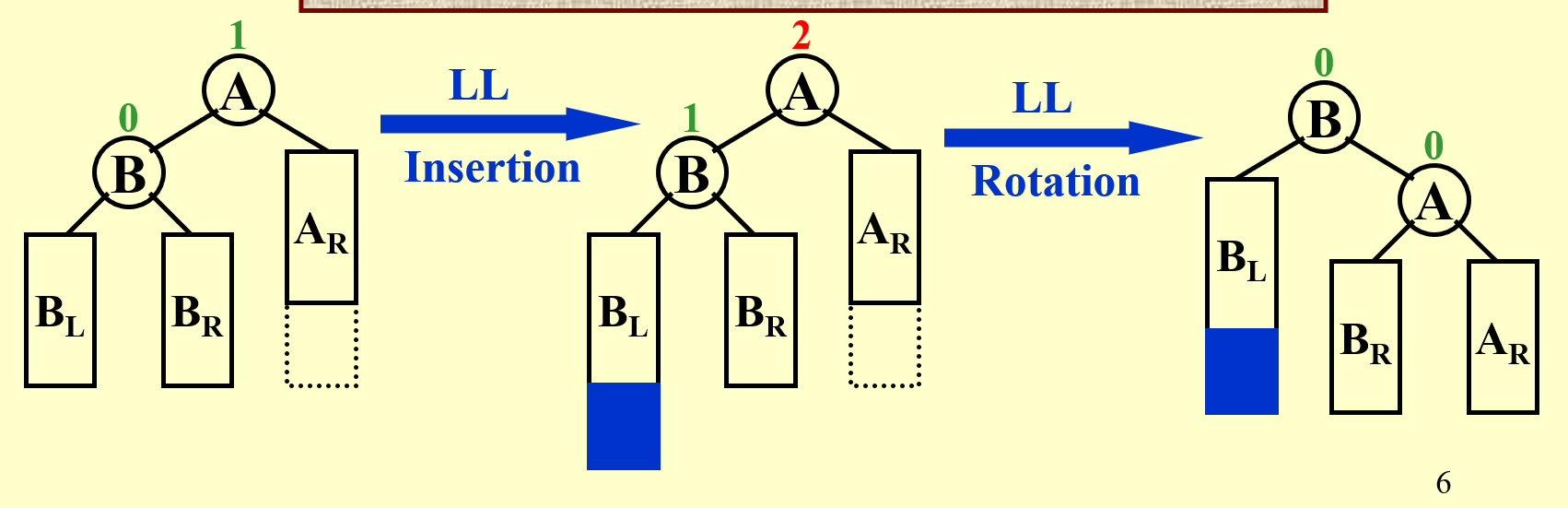
把 B 的右子树连到 A 的左子树上，把 A 作为 B 的右子树。同时要更新父亲。

上面两种叫作 “单旋”。

LR Rotation: Trouble Maker 在 Trouble Finder A 的 LR，即 C；无论在 C 的左子树还是右子树上，都把 C 当成新的根节点。

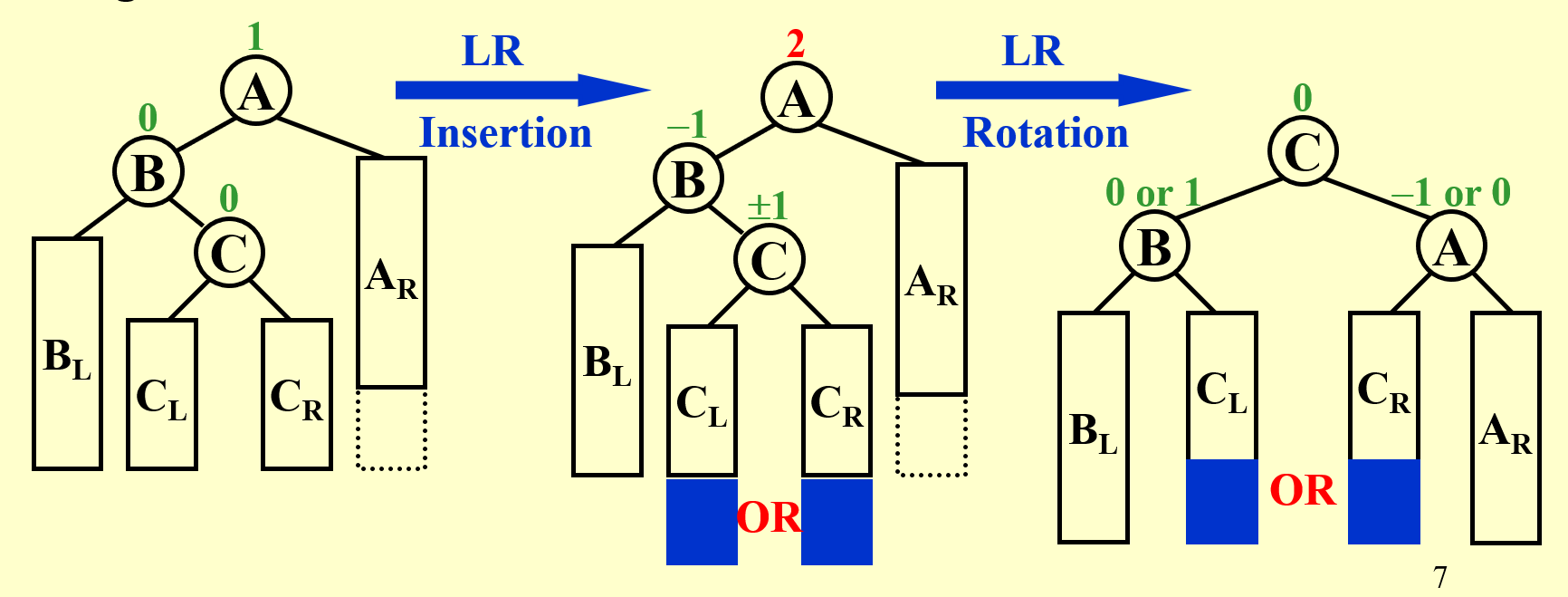
RL Rotation:

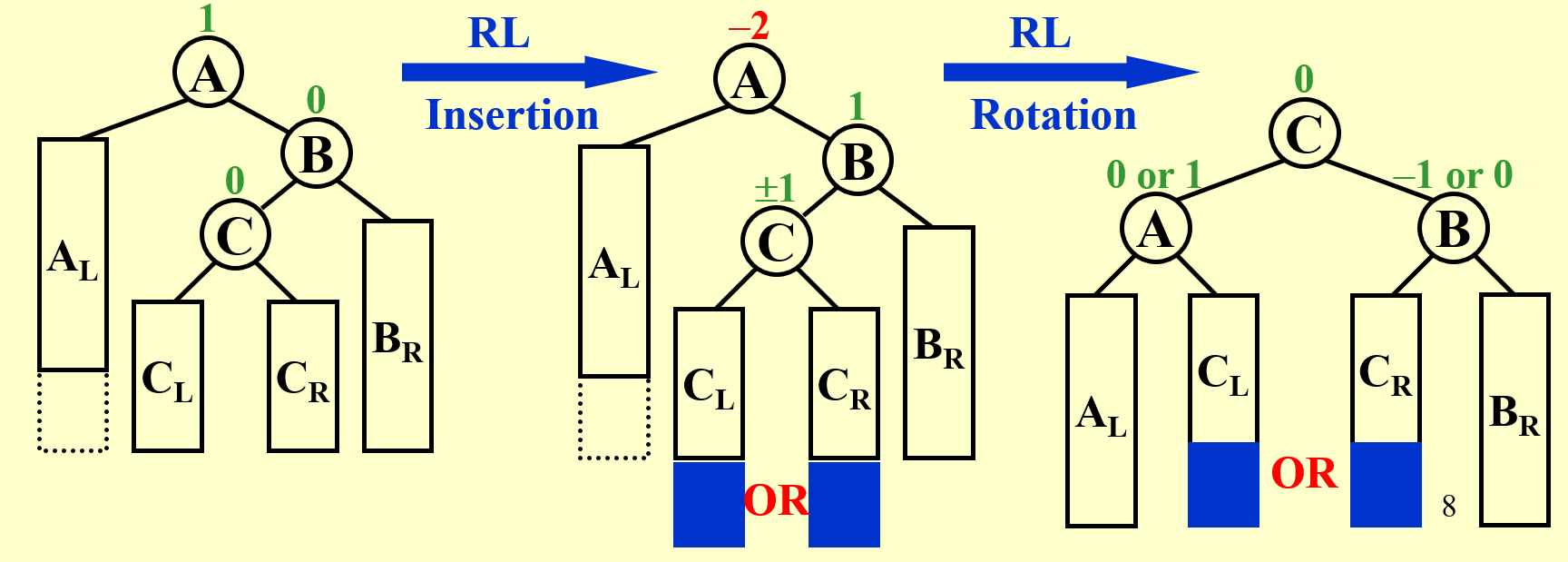
这两种也叫做 “双旋”。

Time Complexity

Let $n_h$ be the minimum number of nodes in a height balanced tree of height $h$ (the height of root is $0$).

高为 $h$ 的树中的最少节点数

我们有递推式：$n_h = n_{h - 1} + n_{h - 2} + 1$

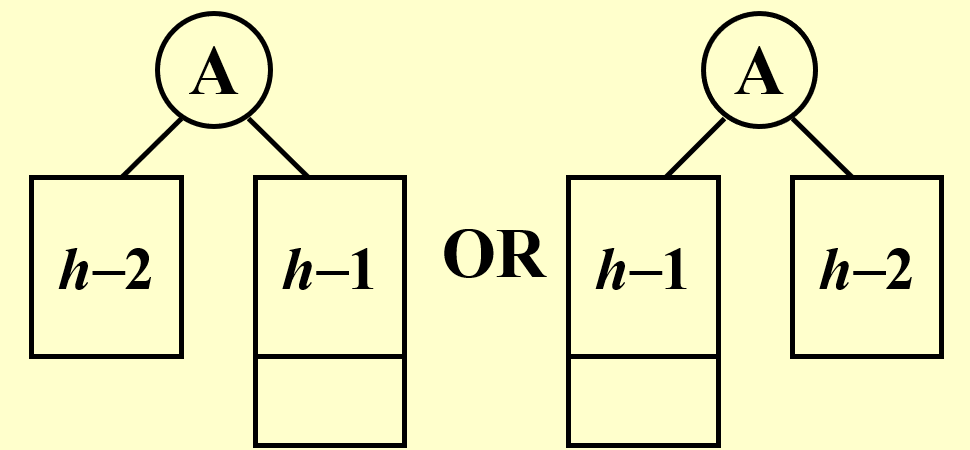
可以证明 $$ n_h = Fib_{h + 2} - 1, \forall h\geq 0 $$ 由 Fibonacci 数列通项公式知，$h = O(\log n)$。

删除：对于叶节点，直接删除；对于非叶子节点的删除，转化为对叶子节点的删除

1. 若一非叶子节点，该节点只有左孩子。操作：该节点的值替换为左孩子节点的值，然后删除左孩子节点。【左孩子节点为叶子结点，所以删除左孩子节点的情况为第1种情况。】【为什么左孩子节点为叶子节点，因为删除节点前，该树是AVL树，由AVL树的定义知，每个节点的左右子树的高度差的绝对值<=1,由于该节点只有左孩子，没有右孩子，如果左孩子还有子节点，那么将不满足每个节点的左右子树的高度差的绝对值<=1，所以左孩子节点为叶子结点】
2. 若一非叶子节点，该节点只有右孩子。操作：该节点的值替换为右孩子节点的值，然后删除右孩子节点。【右孩子节点为叶子结点，所以删除右孩子节点的情况为第1种情况。】【为什么右孩子节点为叶子节点？答案和第二种情况一样】
3. 若一非叶子节点，该节点既有左孩子，又有右孩子。操作：该节点的值替换为该节点的前驱节点（或者后继节点），然后删除前驱节点（或者后继节点）。【前驱结点:在中序遍历中，一个节点的前驱结点，先找到该节点的左孩子节点，再找左孩子节点的最后一个右孩子节点。向左走一步，然后向右走到头。最后一个右孩子节点即为前驱节点】【后继节点：在中序遍历中，一个节点的后继结点，先找到该节点的右孩子节点，再找右孩子节点的最后一个左孩子节点。向右走一步，然后向左走到头。最后一个左孩子节点即为前驱节点】

删除之后，还需要重新平衡，并更新 BF 值，这是 $O(\log n)$ 的。

Assignment

连边的时候，要把连向 father 的和从 father 连出来的，都连好（要注意根的问题）。

要记得转之前，从最下面往上更新 Height

转的时候，要把转的过程中 Height 的改变更新

转之后，要把到根的 Height 更新

同时要维护根，以便找到树在哪

Splay Trees

对于任意 $M$ 个操作，从空树开始逐步完成它们所用的时间最多是 $O(M\log n)$ 的。

AVL Tree 是一种 Splay Tree。

Splay Tree 的每一个操作不一定是 $O(\log n)$ 的，但是 Amotized Time（摊还时间）是 $O(\log n)$ 的。单个操作的时间可能坏到 $O(n)$，但是不会有 $M$ 次一直坏下去，之后的时间肯定跟第一次不一样，在慢慢变好。

在一般的 Splay 中，每次访问了一个节点，就用 AVL Rotation 把它转到根节点。但是，不能只使用单旋，这样可能会使得情况更糟。

旋转

三种情况：X.father = root(Zig), Zig-Zag, Zig-Zig

势能函数：$\Phi(T) = \sum_{t\in T} \log S(t)$，$S(t)$ 表示以 $t$ 为根的子树中点的个数（包括这个根），为便于表示，我们记 $\log S(t)$ 为 $R(t)$，称为 $t$ 的 $\rank$。

Zig:

Zig-Zig: $$ \hat{c} = c + \phi(T_2) - \phi(T_1) $$ 具体计算详见YDS的pdf。

势能函数的改变，可能是负的，因为是SUM S_i，但我们只需要上界即可

查找

每找一个点，就会旋转，旋转一次就往上走两层。所以旋转的次数和往上走的次数是相同的，所以认为查找的次数也是 $O(\log n)$ 的。

插入

插入 -> 转到根

插入的时候，改变过势能的只有从根到插入节点这一条路径上的点（设为 $Y_i$）的势能函数。 $$ \Delta \Phi = \sum \log (S(Y_i) + 1) - \log S(Y_i) = \log\prod \frac{S(Y_i) + 1}{S(Y_i)}\leq \log \prod \frac{S(Y_{i+1})}{S(Y_i)} \ = \log\frac{S(Y_n) + 1}{S(Y_0)} \leq \log n $$ 删除

找到 X 并转到根 -> 删除根 -> 找到左子树中最大的节点并转到根（它一定没有右子树） -> 把原来的右子树变成它的右子树

总结：对于 Splay Tree，我们不关心是否平衡，我们只去闭着眼睛做旋转。

Amotized Analysis

Worst-Case Bound is Stronger than Amotized Bound: AVL Tree 的 Worst-Case Bound 是 $O(\log n)$，但是 Splay Tree 只保证 Amotized Bound 是 $O(\log n)$ 的。

Average-Case Bound is Weaker than Amotized Bound : 一般会加入一些概率假设，假设某一情况发生的概率是多大：如，快排的 Worst-Case Bound 是 $O(n^2)$ 的，但是如果假设任何排列是等概率发生的，Average-Cost Bound 就是 $O(\log n)$ 的

Amotized Bound 没有概率假设，是所有情况的真实平均值。

Aggregate Analysis

总和/总量分析：Show that for all n, a sequence of n operations takes worst-case time T(n) in total. In the worst case, the average cost, or amortized cost, per operation is therefore T(n)/n.

Accounting Method

会计法：When an operation’s amortized cost exceeds its actual cost, we assign the difference to specific objects in the data structure as credit. Credit can help pay for later operations whose amortized cost is less than their actual cost.

把多出来的存起来，再在少的时候还回去 $$ T_{amortized} = \frac{\sum_{i}\hat{c_i}}{n}\geq \frac{\sum_{i}{c_i}}{n} $$ $\hat{c_i}$ is Amortized Cost for each opertion, $c_i$ is Actual Cost, T is an upper bound. $$ \text{credit}_i = \hat{c}_i-c_i $$ 我们可以人为定义一个比真正 Cost 要大的的 Amortized Cost，然后计算这个 Amortized Cost 是否透支信用（我们需要保证这个 Credits 时刻非负），如果不透支，那么我们就可以用人为定义的这个 Amortized Cost 来计算总的 Amortized Cost。

在这里，每一步操作的消耗是不同的，是由我们人为定义得到的。

Potential Method

势能函数法

势能函数可以把当前的结构映射到一个数字，称为这个结构的 Potential（势）。 $$ \hat{c_i} - c_i = \text{credit}i = \Phi(D{\text{after }op_i}) - \Phi(D_{\text{before }op_i}) $$ 实际上是把 Accounting Method 里的 $\hat{c}_i\geq c_i$ 给量化为 $\hat{c}_i-c_i = \Delta \Phi$ 了。

credit 告诉我们，这个操作对当前结构改变了多少 $$ \sum_{i} \hat{c_i} = \sum_{i} \big(c_i + \Phi(D_i) - \Phi(D_{i - 1})\big) = \sum_{i} c_i + \Phi(D_n) - \Phi(D_0) $$ 难点在我们需要定义一个好的势能函数。

对于一些开销大的操作，我们想让他的势能函数尽可能降低。

某一步的势能函数可能是负的，但是总体的势能函数的差肯定是正的???

只要使得 $\Phi(D_n) - \Phi(D_0)\geq 0$，就可以用 $\sum \hat{c_i} / n$ 来作为 Amortized Cost。

一般我们要找的这个势能函数在 $D_0$ 取最小值。

FALSE: For potential method, a good potential function should always assume its maximum at the start of the sequence

Charging Method

Amortized Cost of Operation = Actural Cost + Total Change to past operation + total future change by future ops to this op

e.g. vector 动态开内存

Lecture 2. Red-Black Trees and B+ Trees

Red-Black Trees

平衡树：只要层数是 $O(\log n)$ 即可。

AVL 需要每次都得算，更新代价每次都是 $O(\log n)$，常数大；红黑树用颜色保持平衡，用 $O(1)$ 的 Amotized Cost 即可。

• 根是黑的
• 叶节点(NIL)是黑的，如果叶节点是红的，那就再连上一个黑的 NIL。
• 红色节点的孩子都是黑的（黑的可以连续 但红的不能连续）
• 对每一个点，经过子树到叶节点的每一条路上所经过的黑节点都相同 - 把多余的点做成红色的

Black-Height - bh(X): 从 X 节点到叶节点经过多少黑点（不算它自己）

树的 bh 定义为根节点的 bh，且有上界 $2\ln (N + 1)$：数学归纳法。

https://www.cnblogs.com/LiaHon/p/11203229.html

删除

删除的是根节点，则直接将根节点置为null;

待删除节点的左右子节点都为null，删除时将该节点置为null;

待删除节点的左右子节点有一个有值，则用有值的节点替换该节点即可；

待删除节点的左右子节点都不为null，则找前驱或者后继，将前驱或者后继的值复制到该节点中，然后删除前驱或者后继；

变色：

如果删掉红点，不用变色

如果删掉黑点，？？？

最多三次 可以看回放，worst case

B+ Tree

在数据库中建立**索引**，所有数据都存在叶节点上面，非叶节点都是索引。

Definition A B+ tree of order M is a tree with the following structural properties:

(1) The root is either a leaf or has between $2$ and $M$ children. (2) All nonleaf nodes (except the root) have between $\lceil M/2\rceil$ and $M$ children. (3) All leaves are at the same depth. Assume each nonroot leaf also has between $\lceil M/2\rceil $ and $M$ children.

建树时，按照从下往上的方式建。

Find

直接按照搜索树的索引找

Insert

如果可以直接插入，且满足 between $\lceil M/2\rceil $ and $M$ 个元素，就直接插入；

否则，把中间位置的节点挪到上一层上去，然后把元素插进去，把原来的拆成两半

时间复杂度：

深度：$\lceil\log_{\lceil M/2\rceil}N\rceil$

查找的时候，每一层的时间都是 $\log_2 M$

插入的时候，???

伪代码没有考虑 M-1?

叶节点也是看作有孩子的，所以 Order 为 M 的 B+ 树，叶节点中最少存 $\lceil M/2\rceil-1$ 个数，最多存 $M-1$ 个数。非叶节点也一样，因为第一个数不存，所以如果有 $m$ 个孩子的话，就存后 $m-1$ 个数。

删除：还需要找兄弟，如果有兄弟太少了，就挪一些到兄弟那里：如果旁边节点孩子太少了，就挪过去一些；如果这一整层都已经最少了还在删，就直接去掉这一层。

Lecture 3. Inverted File Index

倒排索引

搜索引擎：BFS爬虫（Hash确定Visit、区分优先级下载） + 建立索引 方便找到 + Ranking

Index 给定一个 Term 后，可以通过 Index 在文章里确定位置

Inverted File 以 Term 为 Index 再进行搜索，而不是从各个 File 开始搜索

但是如果只能记下来某个 Term 在哪些 Docs 里出现，不能记录具体在哪儿，之后再找就还会很慢，所以还需要把位置记录下来。

记录的数据：词频、出现在哪些文档、出现在各个文档的哪些位置

词频的意义：词频越高，其中包含的信息量越少；AND操作从最小频率的 Term 开始求交，速度快

while ( read a document D ) {
    while ( read a term T in D ) {
        if ( Dictionary.Find(T) == false )
            Dictionary.Insert(T);
        Get T’s posting list;
        Insert a node to T’s posting list;
    }
}
Write the inverted index to disk;

• 从 D 里寻找一个 Term：分词，几个字/单词确定为一个 Term；阴阳时态词形变化，字形变化；删除不必要的 Stop Words (a, an, it, to) 但是有些连在一起又是有含义的 To be or not to be；二义性，吃苹果和苹果电脑
• Dictionary 需要是一个数据结构：搜索树（B树、B+树、字典树）/ Hash Map

空间不够时

BlockCnt = 0; 
while ( read a document D ) {
  while ( read a term T in D ) {
    if ( out of memory ) {
      Write BlockIndex[BlockCnt] to disk;
      BlockCnt ++;
      FreeMemory;
    }
    if ( Find( Dictionary, T ) == false )
      Insert( Dictionary, T );
    Get T’s posting list;
    Insert a node to T’s posting list;
  }
}
for ( i=0; i<BlockCnt; i++ )
  Merge( InvertedIndex, BlockIndex[i] );

分布式：不要把所有的东西丢在同一台电脑上算/存，可以把不同的文章放在不同电脑，Docs 随便分

如果 Docs 更新了，怎样随同更新：类似 Git，有一个 Main Index，再加一个类似缓存的 Auxiliary index，汇总起来去搜索 Search Results，一段时间后没有问题了再把 Auxiliary Index 汇总到 Main Index 中。

压缩：？？用时间换空间

Thresholding：需要反应的比较快，首先找出来前k个，然后下一页再出来后面的

Ranking：PageRank?

建立时的速度、查询时的速度、相关性

User happiness

• Data Retrieval Performance Evaluation (数据检索性能评价 after establishing correctness)
  • Response time, Index space
• Information Retrieval Performance Evaluation
  • How relevant is the answer set?Relevance measurement requires 3 elements:

相关性评价三要素：

• A benchmark（典型测试集，基准） document collection
• A benchmark suite of queries
• A binary assessment of either Relevant or Irrelevant for each query-doc pair

	Relevant	Irrelevant
Retrieved	$R_R$	$I_R$
Not Retrieved	$R_N$	$I_N$

精准度 Precision $P = R_R / (R_R + I_R)$

召回率 Recall $R = R_R / (R_R + R_N)$

比如新冠，更关注 Recall，想全部找到；比如刷视频，想找到想找到的，不那么关注有没有找到全部，更关注 Precision

Lecture 4. Leftist Heaps and Skew Heaps

一般的堆：完全二叉树！

好处自动保持平衡，找最值容易；坏处无法查找一个元素

怎样用堆维护中位数？两个堆，一个小根堆维护较大的数，一个大根堆维护较小的数，那么大根堆的堆顶就是大根堆的所有数里最小的，小根堆的堆顶就是小根堆的所有数里最大的；然后在插入时，如果大于大根堆的堆顶，就放入小根堆；否则放入大根堆；如果放多了（两个堆的元素个数差值大于 1），就把小根堆里的东西放到大根堆。

Leftist Heaps

因为一般的堆的性质中，自动保持平衡实际是不需要的，因此这个左式堆并不是平衡树，因为查找的时候也只会涉及堆顶。这只是保证合并速度的优化。

合并两个堆：一般需要 $O(n)$，但是使用左式堆使得变成 $O(\log n)$

一般堆：直接把两个堆丢在一起，然后从最底层的非叶节点开始层序遍历，每遍历到一个节点就让它堆化（让它的子树符合堆的性质，假设它离叶节点的高度为 $h$，则最多进行 $h$ 次即可使得子树堆化）。由于 $h$ 层有 $2^{\log_2{n}-h} = n/2^h$ 个节点，所以乘起来再求和，则 $n\sum_{h=1}^{\log_2{n}}h/2^h = 2n-(2+\log_2(n)) = O(n)$。

Definition The null path length, Npl(X), of any node X is the length of the shortest path from X to a node without two children. Define Npl(NULL) = –1.

Npl(X) = min { Npl(C) + 1 for all C as children of X }

Definition The leftist heap property is that for every node X in the heap, the null path length of the left child is at least as large as that of the right child. 左孩子的 NPL 一定大于等于 右孩子的 NPL

只要证明合并时是 $\log$ 的，那插入的时候就也是 $\log$，可以看作一个节点和一棵树的合并；删除的时候也是 $\log$，可以看作两棵树的合并。

Theorem A leftist tree with r nodes on the right path must have at least $2^r – 1$ nodes.

即，如果一个点的右边的 Npl 路径上有 $r$ 节点，那总共一定要有 $2^r-1$ 节点。

证：右子树的 Npl 路径上有 $r-1$ 个节点，那它最少的情况就是满的，此时会有 $2^{r-1}-1$ 个点，左子树的 Npl 路径也最少 $r-1$ 个节点，最少有 $2^{r-1}-1$。加起来，加上根，是 $2^r-1$。还是归纳法。

Merge 时的两种写法：递归/递推

递归：每次把根小的那棵树的根和左子树留下不动，把右边的子树和那棵根较大的树合并（递归），然后把合并后的整体作为根小的树的右子树，再看左边的 Npl 是不是比右边的大，如果小的话就 swap。

PriorityQueue Merge( PriorityQueue H1, PriorityQueue H2 ) { 
  if (H1==NULL) return H2;
  if (H2==NULL) return H1;
  if (H1->Element < H2->Element)
    swap(H1, H2);  //swap H1 and H2
  if (H1->Left == NULL)
    H1->Left = H2;
  else {
    H1->Right = Merge( H1->Right, H2 );
    if ( H1->Left->Npl < H1->Right->Npl )
      SwapChildren( H1 );  //swap the left child and right child of H1
    H1->Npl = H1->Right->Npl + 1;
  }
  return H1;
}

递推：把所有右路径上的点都作为一个根，只保留它的左子树。然后把所有根按照大小排序，连起来。然后**再从下往上依次看是否需要 swap**，一定记得 SWAP！SWAP 之后就不需要让右路径上的点都在右路径了。

Skew Heaps

Target: Any M consecutive operations take at most O(M log N) time. (N = N1 + N2)

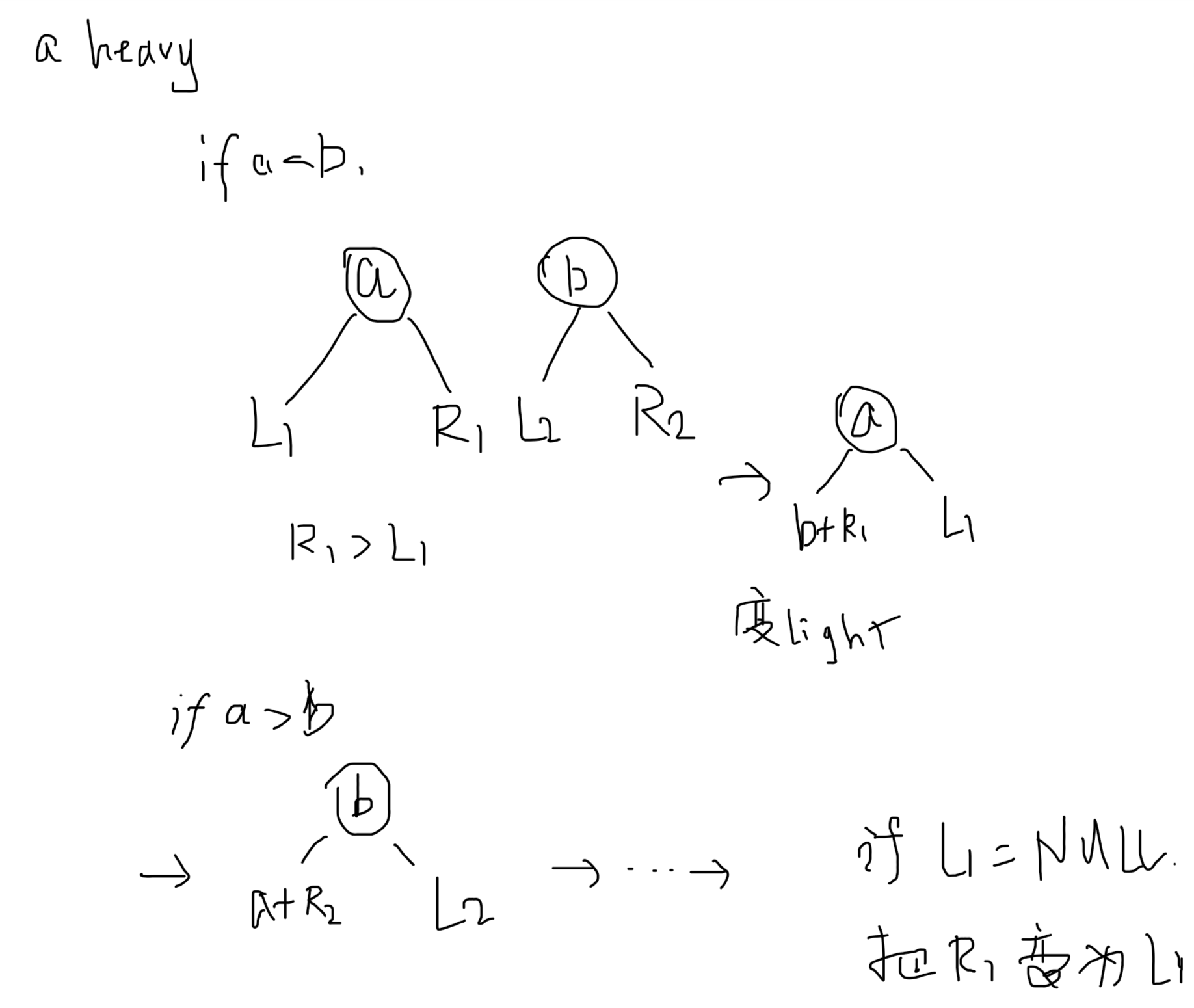
Merge: 每次都换，但是 the largest of all the nodes on the right paths does not have its children swapped.

原来的两棵树右路径上的点，必须要在新树的左路径上；右路径上的 Heavy Nodes 一定变成了 Light Node

Heavy Node: right-heavy - 右子树中的点更多，占整棵树中的点至少一半

要证明合并完之后 heavy 的很少

$\phi(H_i)$ Heavy Node 的 数量

最终的 Amotized：（每一次都是一个，最后求和） $$ \sum\hat{c}_i = \sum c_i + \phi(H_3) - (\phi(H_1) + \phi(H_2)) $$ 定义 $H_i, i = 1, 2$ 中右路径上有 $l_i$ 个 Light Node，有 $h_i$ 个 Heavy Node。显然 $l_i + h_i = \text{right\_path\_nodes\_cnt}$

因为只有右路径上的点才会改变，其他的点都不会变，所以 Actual Cost 可以表示为 $$ \sum c_i\leq l_1 + h_1 + l_2 + h_2 $$ 在变的过程中，可能会有 Light Nodes 变成 Heavy Nodes，但是 Heavy Nodes 一定变成了 Light Node：

$$ \Delta \phi\leq (l_1 + l_2) - (h_1 + h_2) $$ 由此，有 $$ \begin{aligned} \sum\hat{c}_i &= \sum c_i + \phi(H_3) - (\phi(H_1) + \phi(H_2))\ &\leq l_1 + h_1 + l_2 + h_2 + (l_1 + l_2) - (h_1 + h_2)\ &\leq 2(l_1 + l_2) \end{aligned} $$ 而我们可以证明，$l_1 = O(\log n_1), l_2 = O(\log n_2)$。（我们没法证明右路径上 Heavy Nodes 的数量，但是可以证明 Light Nodes 的数量是被控制住的）：使用数学归纳法可以证明，如果右路径上有 $k$ 个 Light Nodes，那这个树至少有 $2^{k} - 1$ 个点。所以 $l_i = O(\log n_i)$。

右路径上的 Heavy Nodes 数量可以任意多。

Lecture 5. Binomial Queue

Binomial Queue

一个 Binomial Queue 由 多个 Binomial Tree - $B_k$ 组成

Queue 中有任意个点，都有对应的二进制表示，所以一定有唯一的对应 Binomial Tree 个数和组成。

• $B_0$ 只有一个点
• $B_k$ 是把两个 $B_{k-1}$ 合并起来，第二个 $B_{k-1}$ 作为 第一个的孩子

性质：

• $B_k$ 的根有 $k$ 个孩子，分别是 $B_0, B_1, \cdots, B_{k-1}$，树高为 $k$（假设根节点 Height = 0）。
• $B_k$ 有 $2^k$ 个节点。
• 深度为 $d$ 的点共有 $C_{k}^d$ 个

操作：

Find Min：找 $k$ 棵树的根，$O(\log n)$

Merge：像加法一样，从 $B_0$ 开始加，要进位。$O(\log n)$

Delete Min：找到最小，把它删掉，把它的孩子和剩下的合并 $O(\log n)$

Insert：一般情况就是特殊的 Merge，如果依次按顺序插入，是 $O(n)$ 的：

证1：只需要看末尾 0 的位置，看最后一个 0 后面有几个 1。末尾是 $0$ 的，有 $n/2$ 个；末尾是 $01$ 的，有 $n/4$ 个；末尾是 $011$ 的，有 $n/8$ 个；... $$ \begin{aligned} nS &= n(1\times \frac{1}{2} + 2\times \frac{1}{2^2} + 3\times \frac{1}{2^3}+\cdots)\ &\leq n(2 - k/2^k - ½^{k-1}) \end{aligned} $$

Expensive insertions remove trees, while cheap ones create trees.

证2：看智云ppt

For a binomial queue, Insertion takes a constant time on average.

Decrease Key：专指已经知道在哪，要把减小它的值

倍增的 Hash Table Amotized Analysis

size(T) Table 的 Size

num(T) 指 Table 中的元素数 $$ \phi(T) = 2\text{num}(T) - \text{size}(T) $$ Insert：

分情况：如果第 $i$ 次 Insert，没有使得表倍增；如果使得表倍增

如果没有使得表倍增，那假定 $c_i=1$， $$ \begin{aligned} \hat{c}i &= c_i + \phi_i - \phi{i-1}\ &= c_i + 2\text{num}{i} - 2\text{num}{i-1}\ &= 1 + 2=3 \end{aligned} $$ 如果使得表倍增，则需要有复制的 cost，$c_i=1+\text{num}_{i-1}$， $$ \begin{aligned} \hat{c}i &= c_i + \phi_i - \phi{i-1}\ &= c_i + 2\text{num}{i} - 2\text{num}{i-1} - (i-1)\ &= 1 + i-1 + 2 - (i - 1)=3 \end{aligned} $$ Delete：

当 $num<size/4$ 时，缩小为 $size/2$

定义 $\alpha$: Load of table - number of table / size of table $$ \phi(T) = \begin{cases} 2\text{num}(t)-\text{size}(T), & \text{if } \alpha(T)\geq ½\ \text{size}(T)/2 - \text{num}(T), & \text{if } \alpha(T)\lt ½ \end{cases} $$

Lecture 6. Backtracking

Shortest Path

从起点终点相遇搜索，大概会比直接单源快 40%。

分层最短路

如果点与点距离太多 空间存不下怎么办？可以使用只存相邻点来求近似解。

负圈图，怎么求无圈最短路？如果所有权都是-1，怎样每个点只经过一次求最短路？哈密尔顿回路

算法分析：正确性近似 - 复杂度 14：30？？？？？

Backtracking

回溯

显然，可以通过枚举所有可行解并一一验证的方法来找到所有可行解；回溯法是逐步填写一种可能，之后如果出现矛盾，再回去换另一种可能，这大大减少了对不可行解的验证。

The basic idea is that suppose we have a partial solution ( x1, ... , xi ) where each xk in Sk for 1 le k le i lt n. First we add x{i+1} in S{i+1} and check if ( x1, ... , xi, xi+1 ) satisfies the constrains. If the answer is “yes” we continue to add the next x, else we delete xi and backtrack to the previous partial solution ( x1, ... , x{i-1} ).

可以找到所有可行解，dp不行。

八皇后

可以认为是博弈，所有二人博弈都可以画 Game Tree，Game Tree 中每条边都是一个决策，点是状态。

重建距离

如果已知数轴上几个点，他们之间的距离共有 $n(n-1)/2$ 个；那么，如果已知这些距离，怎样确定这些点的相对位置？

首先解点的个数 $N(N-1)/2=tot$，然后设 $x_0=0,x_N=\max\text{dis}$，寻找下一个最大的距离，然后推断可能的结果（一定是二分支的，会缩小考虑的范围），检查的时候每确定了一个点，都要和已经确定的点算出距离检查在不在表里。$O(2^n n\log n )$。

如果是环，$O(n^n n\log n)$。

Tic Tac Toe

可以构造函数去评估某个解的 goodness 程度

例如：$f(P) = W_{computer} - W_{Human}$

human 就想去 minimize 这个函数，computer 想去 maximize 它

胜为1，负为-1，平为0。从结果慢慢往上推。

这种博弈里也可以剪枝，$\alpha$ pruning, $\beta$ pruning, 综合被称作 $\alpha-\beta$ pruning，大概只需要搜索 $O(\sqrt{N})$ 个点。

数数 Computer 可能有几行可以赢 - 数数 Human 有几行可以赢。

$\min$ 层，是取第三层的 $\min$，如果 $x\leq 13$，那第二层中间那个应该是 $x$；如果 $x>13$，那第二层中间那个应该是 $13$。因为右边那一支已经有 $9$，所以肯定第二层右边的是比 $9$ 小或等的一个数，那只要第二层中间的是比 $9$ 大的，那最顶层肯定只能选第二层中间的。

Lecture 7. Divide and Conquer

$$T(N) = aT(N/b) + f(N)$$

一般形式，$a\neq b$，$f(N)$ 是 Combine 的时间

子问题，一般会比总问题时间复杂度更低。很多奇奇怪怪的复杂度是用过分治计算得到的。

可解决问题：

• Closest Points Problem: 平面上最近点对
• Merge Sort
• Matrix Multiplication, 分块乘法
• Count Inversions: 逆序对
• Median of n numbers
• FFT: ploy * ploy
• $x^n$
• Convex Hull, 凸包

Asymptotic Analysis 渐进情形分析：

常数隐藏掉，低阶的项也去掉

Machine Model

Random Access Model 中 假定 Arithmetic: +, -, *, /，内存读取等单个单元的操作，都认为是 $O(1)$。

Case: Closest Points Problem

Given $N$ points in a plane. Find the closest pair of points. (If two points have the same position, then that pair is the closest with distance 0.)

1. 预处理时，按照 $x$ 为第一优先级，$y$ 为第二优先级首先排好序。分开时，直接按照下标分成两半，是 $O(1)$ 的。
2. 合并时，对分界线左右两边 $\delta\xlongequal{\triangle}\min(cp(L_x), cp(R_x))$，从 $(-\delta, \delta)$ 的点中，按照 $y$ 排序，每个点都找他下面的 $\delta$ 范围的点。可以证明，如果把 $\Delta x\in(-\delta,\delta), \Delta y\in (0, \delta)$ 这一个区间，划分成8个方形，那每个方形里只有最多 1 个点（常数），所以合并总共是 $O(n)$ 的。
3. 合并时的“按照 $y$ 排序”，可以提前把所有点按照 $y$ 排序进行预处理，然后每次合并时，只需要依次扫描这个预处理表中的点，判断和分界线的 $\Delta x$ 是不是在 $(-\delta, \delta)$ 范围内。这样就可以 $O(n)$ 取得按 $y$ 顺序的点。

$T(N) = aT(N/b) + f(N)$

归纳假设

首先猜一个，然后去证明它对不对，如 若假定 $T(N) = O(g(N))$，那么 $T(N)\leq cg(N)$

于是我们就可以假定 $T(N/b)\leq cg(N/b)$，看能否推出 $T(N)\leq cg(N)$，$c$ 只要存在即可，不需要对任意的 $c$ 都满足。

especially. $c$ 必须是一致的，如果从 $T(N/b)\leq cg(N/b)$ 只能推出来 $T(N)\leq (c+1)g(N)$，那肯定是不对的。

递归树

假定每个节点，都是代表 $f(N)$，然后最后把所有节点的时间从下往上加起来就好。

所以如果一个点，它本身是 $f(N)$，那它有 $a$ 个孩子，每个孩子都是 $f(N/b)$，孙子就是 $f(N/b^2)$。 $$ T(n) = f(n) + af(n/b) + a^2f(n/b2) + \cdots + a^Lf(n/bL) $$ 我们知道分到最后肯定是 $O(1)$ 的，那么 $1=n/b^L\Rightarrow L = \log_b n$。

就 $T(N) = 2T(N/2) + N$ 而言，这里 $af(N/b)=f(N)$，所以有 $$ T(N) = N + N + N + \cdots + N=N\log_2N $$ 总共 $L = \log_2N$ 个 $N$ 加起来。

一般地，如果 $af(N/b)=f(N)$，有 $T(N) = f(N)\log_bN$，相当于每层复杂度都一样，就是要乘 层数。

如果是 $af(N/b) = \kappa f(N), \kappa<1$，那么有 $T(N) = O(f(N))$，证明： $$ \begin{aligned} T(N) &= f(N) + af(N/b) + a^2f(N/b2) + \cdots + a^{\log_b N}\times 1\ &= f(N) + \kappa f(N) + \kappa^2f(N) + \cdots + \kappa^{\log_b N}f(N)\ &= f(N)\frac{1-\kappa^{1+\log_bN}}{1-\kappa}\ &= \frac{1}{1-\kappa}f(N)-\frac{\kappa}{1-\kappa}N^{\log_b\kappa}f(N) = O(f(N)) \end{aligned} $$ 如果是 $af(N/b) = K f(N), K>1$，相当于 $f(N) = O(N^{\log_ba-\epsilon})$，那么有 $T(N) = O(N^{\log_ba})$ $$ \begin{aligned} T(N) &= f(N)\frac{K^{1+\log_bN}-1}{K-1}\ &= \frac{K}{K-1}N^{\log_bK}f(N) - \frac{1}{K-1}f(N) \end{aligned} $$

用到一个恒等式：$a^{\log_b N} = (a^{\log_aN})^{-{\log_a b}} = N^{\log_b a}$

更特殊的： $$ T(N) = 2f(N/2) + \frac{n}{\log n} $$ 计算 $af(N/b)$ 有 $$ 2\frac{n/2}{\log n-\log 2} = \frac{n}{\log n-\log 2}\neq \frac{n}{\log n} $$ 所以并不是刚刚的情形，使用递归树

另外一个题：

$$ T(N) = 8 + 8^2 + \cdots + (N/M)^3f(N/2t) + 8^{t+1}M =N^3/M2 $$ $N/2^t = \sqrt{M}\Rightarrow t = \log_2N/\sqrt{M}$

再例 $$ T(N) = \frac{12}{5}N + T(\frac{N}{5}) + T(\frac{7N}{10}) $$ 递归树： $$ \begin{aligned} T(N) &= \frac{12}{5}N + \frac{12}{5}(\frac{N}{5}) + \frac{12}{5}(\frac{7N}{10}) + \frac{12}{5}(\frac{N}{5})^2 + \frac{12}{5}(\frac{7N}{10})^2 +\cdots\ &= \frac{12}{5}N(1 + \frac{9}{10} + (\frac{9}{10})^2+\cdots) = O(N) \end{aligned} $$ 再例 $$ T(n) = 2T(\sqrt{n}) + \log n $$ 不妨设递归树总共 $M$ 层，则 $n^{(1/2)^M} = 1 + \epsilon$，$(1/2)^M = \log_n(1+\epsilon)\Rightarrow m = \log_{1/2}\log_{n}(1+\epsilon)$，所以总共的时间复杂度 $T(n)$ 即为层数 $\times$ 每层复杂度为 $\log n$，总共 $\log n\times \log\log n$。

或者，换元，令 $k=\log_2(n)$，则 $$ T(2^k) = 2T(2^{k/2}) + k\ U(k) = 2U(k/2) + k\ T(2^k) = U(k) = k\log k = \log n\log\log n $$ 主定理，要再看看ppt里另一个形式，看看能不能凑到 $O(n^t)$ 的 $t$ 里。

比如 $T(n)=3T(n/3)+n/\lg n$，$O(n^{1-\epsilon})$ 里，找不到一个 $\epsilon$ 使得 $n=O(n^{1-\epsilon})$

Lecture 8. Dynamic Programming

分治法当中，子问题和原问题之间是有阶数/倍数差异的，而子问题和原问题是独立的。

动态规划中，子问题和原问题的差异是很小的，一般只相差常数个单位，但是子问题和原问题之间是相关的，是有很多重复的。

1. Characterize an optimal solution
2. Recursively define the optimal values
3. Compute the values in some order（计算值）
4. Reconstruct the solving strategy（重新回去找到解，即怎样得到值的过程）

两种方法：

• Memorization (Top Down)：记忆化搜索，如果发现当前要解决的问题之前解决过了，就直接用之前记下来的结果
• Tabulation (Bottom Up): 直接构造表，但是要去构造 Order，要对问题有更清晰的理解。

差异：Coding Complexity, Speed, Stack Space, Find Order Manually.

Case: Matrix Multiplications

矩阵乘法中，如果 $M_{a\times b}\times N_{b\times c}$，那时间复杂度是 $O(abc)$，即进行 $abc$ 次乘法。 假设现在有 $n$ 个按顺序排好的矩阵，我们要想加括号，让算出整个结果的速度更快。如果我们想算出方案数，设方案数为 $b_n$，则 $$ b_n = \sum_{i=1}^{n-1} b_i b_{n-i}, \text{ where } n\gt 1, \text{and }b_1 = 1 $$ 这事实上是 Catalan 数，它是 $O(4^n/n\sqrt{n})$ 的。

那回到问题本身，我们不只是想算出方案数，我们想算出来 Cost，那么设 $m_{i,j}$ 为从第 $i$ 个乘到第 $j$ 个的最优 cost，则如果设 $M_i$ 的维度为 $r_{i-1}\times r_i$，那么有 $$ m_{ij} = \begin{cases} 0, &\text{if }i = j\ \min_{i\le l\lt j}(m_{i,l} + m_{l + 1, j} + r_{i - 1}r_{l}r_{j}), &\text{if }i < j\ \end{cases} $$

Case: Floyd-Warshall Algorithm

定义 $D^k_{i,j}\xlongequal{\triangle} \min_{l\le k}(\text{length of path from node}_i\text{ through node}_l\text{ to node}_j), 0\le k\lt n$，$D^{-1}_{i,j}\xlongequal{\triangle} cost_{i,j}$。

中间节点的最多个数

Order：$D^{-1}\to D^{0}\to\cdots D^{n-1}$ $$ \begin{aligned} D^k_{i,j} &= \begin{cases} D^{k-1}{i,j}, &k\notin \text{ the shortest path from node}_i\text{ through node}_l\text{ to node}_j\ D^{k-1}{i,k} + D^{k-1}{k,j}, &k\in \text{ the shortest path from node}_i\text{ through node}_l\text{ to node}_j\ \end{cases}\ &=\min(D^{{k-1}_{i,j},D}{k-1}{i,k} + D^{k-1}_{k,j})\ \end{aligned} $$ 实际计算时为什么不需要存 $k$ 这一维？

第 $k$ 行和第 $k$ 列在计算 $D^{k}$ 时是不会变的，它一定等于 $D^{k-1}$ 时的值，所以更新时用到的实际就是 $D^{k-1}$ 时的值。

Case: Product Assembly

Two assembly lines for the same car Different time for each stage One can change lines between stages Minimize the total assembly time

两条流水线，

每个阶段时认为都是在当前阶段上 Optimal 的，然后利用之前阶段的来计算当前阶段最优解。

Other Cases in Slides

背包

用前i 个物品正好获得收益p 所需要最小总空间。最后只需要算出使得W(i,q) <= M 的最大的q 即可。

Lecture 9. Greedy Algorithms

Make the best decision at each stage, under some greedy criterion.

Case: Activity Selection Problem

有好多任务，$s_i$ 开始，$t_i$ 结束，同一时刻只能做一个任务，问最多做多少个及方案

贪心算法：按照结束时间排序。

可以通过反证法来证明贪心算法和最优解是等价的

Case: Huffman Codes

Lecture 10. Computational Complexity

NPC：

只关注可计算的问题。

给一个 Problem X，和一个 Machine Model M，使用 M 需要花多久去解决 X？

P 问题：Polynomial Time，多项式可解，认为是 Tractable / 简单的。多项式时间内可以得到解，也一定可以验证解，$P\sub NP$，问题是无法证明 $P$ 是 $NP$ 的真子集。

NP 问题：Nondeterministic Polynomial Time，多项式时间内可验证一个解是否正确，认为是 Intractable / 难的。它可能是多项式可解的，也可能不是多项式可解的。

NP-C 问题：是 NP 问题的一个子集，且所有的 NP 问题都能多项式归约到 NP-C。NP-C 至少是和 NP 一样难的，即如果 NPC 多项式可解，那 NP 也多项式可解，即 NP 可以多项式时间内 Reduction 到 NP-C 问题。在证明 NP-C 问题时，我们一般证明 $\Omega$ 复杂度，因为是要证明它有难。

现在没有办法证明 P 是否与 NP-C 有交集，因为如果有交集，那 P = NP，NPC 是其中的一个子集；如果没有交集，那 P $\neq$ NP。

NP-Hard 问题：代表所有的 NP 问题都能多项式归约到的集合。不一定是 NP 问题，不一定是 Decision Problem，即它可能在多项式时间内不可验证。NP 和 NP-Hard 的交是 NP-C。 所有问题都不比 NP-Hard 难。

co-NP 问题：补是 NP

问题分类：

Decision Problem: Output YES / NO

Search Problem: Output YES / NO and Solution 可行解

可以把 Optimization Problem 转化为 Decision Problem，比如要想求 $\min$，那只需要构造多个 Upper bound，即可变成多个判定问题。Optimization Problem + $k \in \mathbb{R}$ => Decision Problem。

例子：

第一个 NP-C 问题 Set Problem: 用逻辑运算构造一个表达式，如果给某个变量赋值之后，可以一定让整个表达式值为 1。SAT 问题是指给定一个包含n个布尔变量的逻辑式，问是否存在一个取值组合，使得该式被满足

编码：Encoding

背包问题中的 W，实际上是指数，所以背包问题仍然不是多项式可解的。

Def. Language $L$, the formal realization of a problem.

If $x\in L$, the answer is YES; if $x\notin L$, answer is NO.

Turing Mechine: the formal analogue of an algorithm. 可以进行按步骤的运算

比如要证明一个数是质数还是合数，那如果证明合数，只需要给出因子就得证，但是质数复杂得多。

2set 是 P 问题，3set是 NP-complete 问题

Reduction 化简归约

NP-complete 指 Decision Problem，它一定是 NP 问题，不需要证明；NP-hard 需要证明是 NP，它不是 Decision Problem

• Turing Reduction / Cook Reduction

不断调用 B 去解决 A，那 B 至少跟 A 一样难，$A\leq_P B$。

• Karp Reduction

$L_1\leq_PL_2$ 即 $x\in L_1\iff f(x)\in L_2,$，$L_1,L_2$ 都是 $\{0,1\}$，$x\in L_1$ 代表 $x$ 的 Decision 是 1，那 $f(x)$ 一定也是 1；如果 $x\notin L_1$，即 $x$ 在问题 $L_1$ 中答案是 0，那 $f(x)\notin L_2$。

多项式归约具有传递性

所以 NP-Complete 集合里的所有问题，都可以互相多项式归约；所以如果要证明一个问题是 NP-Complete 的，那只需要证明某一个 NP-Complete 可以归约到它上面。

近似比是不能多项式规约的。

Mid-term Contest

In the knapsack problem, we have n items, in which the i-th item values v_i and sizes s_i, and a knapsack capacity C. (All positive integers.) Our goal is to select a subset of the items such that the total value of the items should be as large as possible, and their total size should be at most C. We will design dynamic programming to solve this problem. Please choose the correct description of subproblems of an optimal solution.

Let $OPT(i,v)$ denote the smallest size of a subset items 1,…,$i$ such that its value is exactly $v$, If no such item exists it is infinity.

另一种背包，时间复杂度是 $O(N\times totVal)$

In this problem, we would like to find the amortized cost of insertion in a dynamic table T.

Assume that entering an element in an empty slot of a table costs 1, and copying an element from a table into a new table also costs 1.

When an item is inserted into a full table, the table T is expanded as a new table T′, and ∣T′∣=∣T∣+10000, i.e, each new table has 10000 more slots than the previous one. Then, we copy all the elements of the old table T into this new table T′, and insert the item in the new table.

Starting with an empty table T with 10000 slots, we insert a sequence of n elements. What is the amortized cost per insertion? (Choose the smallest upper bound that applies)

只是扩大常数个，不是扩大一倍；可以直接当成每次增加 1 来想，每放进来一个就又满了，又要 copy 一遍。

Lecture 11. Approximation

Definitions

Approximation Ratio: 最优化的问题的近似解与最优解的比（关心解的质量）

近似比越小越好，越接近 1 越好。近似比一定大于1 ！！！

对于一个 Instance $I$，如果 $C(I)$ 是近似算法的解，$\mathit{OPT}(I)$ 是最优解。那么求最小值问题的近似比 $\alpha = \sup_{I}\dfrac{C(I)}{\mathit{OPT}(I)}$，求最大值问题的近似比 $\alpha = \sup_{I}\dfrac{\mathit{OPT}(I)}{C(I)}$

Approximation Scheme: 定义？？？

FPTAS (fully polynomial-time approximation scheme): 那个关于 $1/\epsilon$ 的多项式，不在指数上；PTAS (polynomial-time approximation scheme): $1/\epsilon$ 在指数上

实际应用时怎么求 Approximation Ratio？ $$ \alpha = \sup_{I}\dfrac{C(I)}{\mathit{OPT}(I)}\leq \sup_{I}\dfrac{C(I)}{\mathit{OPT}'(I)} $$ 其中 ${\mathit{OPT}'(I)}$ 表示 Lower Bound，下界。

如果有 2 个在线近似算法，那如果每一步都随便拿一个来用，那可能最后比只用一个的近似比还烂。

Approximate Bin Packing

装箱问题：每个箱子大小为 $1$，有 $N$ 个物品，要全装进去，问最少装几箱？

3 种离线算法

Next Fit：如果当前的最后一个箱子能放就放，放不下就开辟新箱子

Th. 如果最优解为 $M$，那这个算法的解一定不会大于 $2M-1$，所以近似比为 $2$。比如有 $2M-2$ 个 $\epsilon$，有 $2M-2$ 个 $1/2$，最优解为 $M-1$ 个满箱子 + $1$ 个全装 $\epsilon$。

First Fit: 找到第一个能放得下的，放进去。解一定不会大于 $17M/10$。

Best Fit: 在能放的下的箱子里找容量最小的，放进去。解一定不会大于 $17M/10$。

离线算法的近似比一定大于 $1.5-\epsilon$，在线算法最优近似比为 $5/3$。

如果去掉队列中的一个物品，可能 First Fit 最后会让箱子数增加。

如果箱子变大了，那 First Fit 也可能让最后箱子数增加。

Online Algorithms

Th. 任何在线装箱问题的算法，近似比都不低于 5/3

Proof. 假设每个箱子大小为 50，一个输入是 34 个 tiny items

1. 任何好的在线算法面对最初的 34 个 tiny items 都不能装两个箱子，因为如果算法想要装在两个箱子，那输入序列长度为 2，那这个算法的效果就很差
2. 假设之后是 2 个 17，那任意一个近似算法要么是装在一起，要么是装在 2 个箱子里。
3. 如果装在一起，那假设后面的输入是 3 个 26，那最优解为装 3 个箱子，近似算法最好只能装到 5 个箱子
4. 如果装在 2 个箱子里，那假设后面的输入是 2 个 34，那最优解为装 3 个箱子，近似算法最好只能装 5 个箱子

想要去估计最大生成树 $T$ 中的每个边的权值，我们设 $S$ 为每个节点的最大边的集合。$S$ 中每一条边，肯定是某一个端点的最大权边

但是如果改为 $w(S)\geq 0.5w(T)$，这个选项才有意义

这里任意两点之间都可以有路，所以可以构成一个满足三角不等式的度量空间。最差情况，每个最小生成树上的边都走两遍，这样刚好从起点出发，回到起点，所以近似比可以是 2。但是实际上可以在 dfs 基础上再优化，近似比可以更小。

bfs (Level Order) 是不行的，它不会构成一个圈，因为最后回不到原点。

Knapsack

贪心算法1：单位价值最高的选进来。近似比很差，比如背包容量为 $1$，有 2 个物品，一个价值为 $1$，体积为 $1$，一个价值为 $w\lt 1$，体积为 $\epsilon\lt 1$，最优算法的解为 $1$，但是贪心算法1的解为 $w$，近似比为 $1/w$，它可以很大很大。

贪心算法2：价值最高的选进来。近似比还是很差，因为可以有许多性价比为 $1$ 但是体积很小的的物品，但是有一个体积为 $1$，性价比为 $t\lt 1$ 的物品，那会优先选这个大的，导致近似比为 $1/t$，可以很大很大。

ModiedGreedy 改进的贪心算法：前两个贪心的解取 $\max$。近似比为 $2$。

证明：假设 $k$ 个物品的性价比满足 $$ \frac{v_1}{w_1}\geq \frac{v_2}{w_2}\geq \cdots\geq \frac{v_k}{w_k} $$

PTAS: $\epsilon$ 一定

FPTAS: 通过对另一种背包的改进，$O(N\times totVal)$，

Load Balancing

$m$ 个机器，$n$ 个工作 ($p_1, \cdots, p_n$)，需要尽量负载平衡，让全部完成的时间尽可能短。

显然 $\mathit{OPT}\geq \max(p_{max}, \sum p_i/m)$。估计近似比的时候往往需要估计最优解的下界。

假设近似算法的解为 $\mathit{AIG}$，设存在这样一种情况，前 $n-1$ 项工作都均匀分好，第 $n$ 项单独留出来了，那 $\mathit{AIG}=\sum_{i=1}^{n-1}p_i+p_n\xlongequal{\triangle}x+p_n$。而 $\mathit{OPT}\geq \max(p_n,\dfrac{mx+p_n}{m})\geq x+p_n/m$，那么有 $$ \mathit{AIG}=x+p_n/m+(1-1/m)p_n\leq \mathit{OPT}+(1-1/m)\mathit{OPT}=(2-1/m)\mathit{OPT}\leq 2\mathit{OPT} $$

K-center

把 $n$ 个点，划成 $k$ 个圈，让最大半径最小。

近似解如果在最优解的圈里，那只要以他为中心画一个半径为 $2r$ 的圈，那一定可以把所有的点都圈进来。

Lecture 12. Local Search

已经有了一个算法可以得到可行解，能不能让这个解的近似比更好一些？

如果把解的近似比当成函数，那可以选取随机梯度下降的方法，但是有时候近似比函数不是单峰的，或者存在鞍点，那这样就会出问题。

对 NPC 问题很难找到最优解，P 问题会更容易找到最优解。

Hopfield Neural Networks

图里每个点都有 +1,-1 两个状态，每个边，如果节点的状态相同，那这个边就是负边；如果状态相反，那边是正边，每个边的权值绝对值代表需求的重要性。

想要让这个图是足够好的。

如果 $w_e\times s_{u}\times s_v\lt 0$，那这一条边 $e$ 是好的，如果与一个节点相连的所有边的好边的加权和比坏边的加权和要大，那就称为这个节点是满意的。如果图里所有的点都是满意的，那这个图就是稳定的。

稳定：所有人都满意，都不想改。

如果把自己的状态改了，那一定可以让自己从不满意变成满意。

Th. 这个图在改变最多 $\sum|w_e|$ 次之后一定会稳定。

Decision Problem 是 P 的，但是 Search Problem 是难的。

质数合数问题也是这样，判断是容易的，但是找到因式分解是难的。

Maximum Cut Problem

把图分成二部图，想让割最大。

一个近似算法：假设隔成 A,B 两部分，对于所有的 $u\in A$，只要 $\sum_{v\in A} w_{uv}\gt \sum_{v\in B}w_{uv}$，就把原来的割换掉，把 $u$ 挪到 B 里。

优化：Big-improvement-flip

只有 $\sum_{v\in A} w_{uv}\gt \sum_{v\in B}w_{uv}+\dfrac{2\epsilon}{n}w(A,B)$ 才换。

Homework

不止2倍，可以任意大。假设有点 (0,0), (w,0), (w,h), (0,h) 假设最开始先找到的中心是 (-1,h/2), (w+1,h/2)，那分类是把 (0,0),(0,h) 分在一起，但是正解应该是把 (0,0), (w,0) 分在一起。

A. 分成两个相等的集合，就是 NP。

D. 假设有一个时间特别特别长

B. 如果每次移最大的，那只要移动过就不会再移回来，所以最多 $n$ 次。

Lecture 13. Randomized Algorithms

避免最坏情况，在一些最坏情况比较差的算法中寻找平均情况最优。

快排的时间复杂度的期望为 $N\log N$，在选主元的时候是按照均匀分布选的。

Amotized 是对最坏情况平均。

两类随机算法：输入是随机的，Average-case；算法是随机的，Randomized Algorithms

Randomized Algorithms 中有两类：拉斯维加斯、蒙特卡洛；分别对应：结果总是正确但是时间不同，时间是相对稳定的但是结果正确性不同。

Example. Hiring problem

Interviewing Cost: $C_i$, Hiring Cost: $C_h$; 且 $C_h$ 远大于 $C_i$。

假设 $M$ 个被雇佣，则总的时间为 $NC_i+MC_h$。现在有一个算法，想找 best，找到 best 就雇佣，把之前的解雇，这样最差时间为 $NC_i+NC_h$。

计算平均情况：设 $X$ 为雇佣的人数（最终只雇佣 1 人，其他 $X-1$ 会被解雇）

为什么是 $1/i$ ? 前 $i$ 个里它最大。

Online: 首先查看前 k 个之后确定一个 best，然后之后的只要大于 best 就直接要，后面的就不看了。

这个算法时间是稳定的，但是正确率不稳定，所以要求使用这个算法雇佣到正确的人的概率。

设事件 $S_i$ 为，正确的人就是 $i$，且这个算法中它被雇佣了，意思就是 $[k+1,i-1]$ 的人都没被雇佣且它比之前探索区间的的最大值要大；即需要保证，[1,i-1] 中的最大值出现在 [1,k] 之间。最后的结果就是 $\mathrm{E}S = \mathrm{E}[\sum S_i]=\sum\mathrm{Pr}(S_i)$。

显然，$S_i=0,i\leq k$。 $$ \mathrm{Pr}(S_i) = \mathrm{Pr}(正确的人就是 i)\mathrm{Pr}(被雇佣) = \frac{1}{N}\frac{k}{i-1} $$

$$\mathrm{Pr}(S) = \sum_{i=k+1}^N\mathrm{Pr}(S_i) = \sum_{i=k+1}^N\frac{1}{N}\frac{k}{i-1} = \frac{k}{N}\sum_{i=k}^{N-1}\frac{1}{i}\geq \frac{k}{N}\ln(\frac{N}{k})$$

当 $k=1/e$ 时，可以让下界最大。

Quick Sort 每次选定一个主元，小于的放左边，大于的放右边，然后递归的去算，求平均耗时。

衡量时间的方式：元素之间比较的次数 = $\sum x_{ij}$，$i,j$ 表示从小到大排好之后的下标。 $$ x_{ij} = \delta_{a_i\text{ compare with }a_j} $$

$$\mathrm{E}X = \sum_{i}\sum_{j>i} \mathrm{Pr}({a_i\text{ compare with }a_j})$$

只有当 $a_i$ 或者 $a_j$ 分在同一个集合的时候，$a_i$ 或者 $a_j$ 做了主元，才会进行比较。所以也就意味着 $a_{i+1}, \cdots, a_{j-1}$ 都在同一个集合里。 $$ \mathrm{Pr}({a_i\text{ compare with }a_j})\leq \frac{2}{j-i+1} $$ 每个都是等概率被选为主元的，只有选了 $a_i$ 或 $a_{j}$ 为主元，才会造成 $x_{ij}=1$，所以概率恰为 $2/(j-i+1)$。

Modified Quicksort 选主元的时候，只有这个主元能够让小的大的的元素数都 $>1/4$，才选。

这样的算法中，选主元的次数符合参数为 $1/2$ 的几何分布（前 $k-1$ 次不成功，最后一次成功），所以几何分布的期望次数为 $2$。每次都可以让下一层的大小最大变为 $n\times 3/4$。所以最多 $\log_{4/3}n$ 层。

ppt 是啥？

Lecture 14. Parallel Algorithms

Parallel Random Access Machine (PRAM) 并行随机访问

所有机器都有共用的 Memory。

for P_i, 1 <= i <= n pardo
    A(i) <- B(i)

正常会需要 $n$ 的时间，并行只需要 $1$ 的时间。

同时读是没问题的，但是如果同时写，写的东西还不同，就需要定义一些规则解决冲突。

读写分类 Exclusive-Read Exclusive-Write (EREW) 独占读独占写；CREW 并发读独占写；CRCW 并发读并发写

再如，把 $n$ 个数加起来，如果非并行，那需要花费 $n$ 的时间，并行只需要花费 $\log n$ 用类似二叉树结构。

Work-Depth (WD)

会出现 $W(n)$ 很小，但是 $T(n)$ 很大的情况

Work load – total number of operations: W(n) 操作数 Worst-case running time: T(n)

W(n) operations and T(n) time P(n) = W(n)/T(n) processors and T(n) time (on a PRAM) W(n)/p time using any number of p ≤ W(n)/T(n) processors (on a PRAM) W(n)/p + T(n) time using any number of p processors (on a PRAM)

$$\sum \lceil w_i/p\rceil = \sum (1+\frac{w_i}{p}) = \frac{\sum w_i}{p} + T(n) = \frac{W(n)}{P(n)} + T(n)$$

Example 前缀和

并不是二叉树，这里也是只需要把最多两项加起来，但是 $B(1,2)$ 代表1加到4，而不是第3和4加起来。

Example Parallel Merge Sort

$$T(n) = T(n/2)+O(n)$$

怎样把合并操作减复杂度？

分成没有交叉的一块块，相当于知道了各自的位置，知道了A序列中有几个空，这些可以填进B序列中的元素。

每一块大小都是 $\log n$ 的，分成 $p=n/\log n$ 块。

从 A 中选一块中的第一个元素，找到它在 B 中的位置，通过二分，这个查找是 $\log$ 的。

然后对于每一块里的所有元素，都可以确定 rank。

这样时间优化为 $$ T(n)=T(n/2)+O(\log n) $$ 但是总 Work Load 依然是 $$ W(n) = 2W(n/2) + O(n) $$

Example 找最大值

法1：最开始全都是 0；然后两两比较，如果小了就给它写1；正确处理写入冲突即可；剩下的那个唯一一个0就是答案；这样只需要 $N^2$ 个 Processer 就可以在 $O(1)$ 做完。这个算法中 $T=O(1),W=O(n^2)$。

法2：分成 $\sqrt{n}$ 个大小为 $\sqrt{n}$ 的块，这样每个块内用朴素的 $T=O(\sqrt{n}),W=O(\sqrt{n})$的算法，然后合并的时候用 $T=O(1), W=O((\sqrt{n})^2)=O(n)$ 的算法，这样即可优化为： $$ W(n) = \sqrt{n}W(\sqrt{n}) + n\Rightarrow W(n) = O(n\log\log n) $$

$$T(n) = \sqrt{n}T(\sqrt{n}) + 1\Rightarrow T(n) = O(\log \log n)$$

法3：分成 $n/\log \log n$ 个大小为 $\log\log n$ 的块。这样 $T(n) = O(\log \log n),W(n) = O(n)$。

$T,W$ 中的 $\log\log(n/h) $ 利用法2来计算得到。

Lecture 15. External Sorting

外排：没办法把所有东西都读进内存，怎么排序？考虑磁带的情况。

Run: 读的一个区间叫做一个 Run

Pass: 读完一遍叫做一个 Pass

按照 Fibonacci 数列的方式放，效率最高

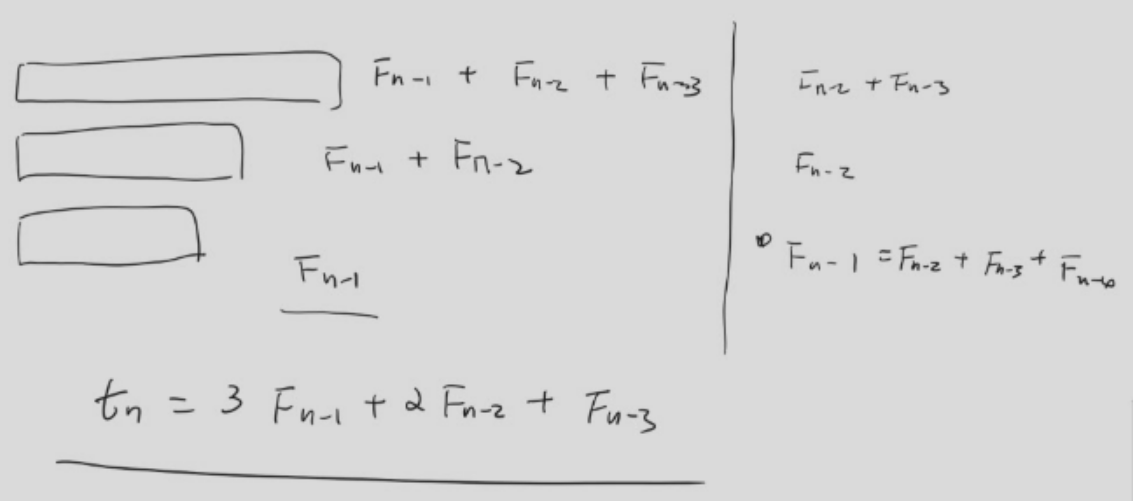
总数应该满足 $3F_{n-1}+2F_{n-2}+F_{n-3}$。

run的长度可以比内存长度大，因为只要 output buffer 写满之后就直接存出去就好。

对于 $k$-way 的 Merge，一般需要至少 2k 大小的 input buffer。

Read Write Merge 是可以并行操作的。

怎样获得一个更长的run？

直接从一个序列读呀读，然后如果发现放不进 output 就在 buffer 中 mark 一下，直到所有的都被 mark，那就重新开始一个新的 run。

Final Exam

判断 13 2pts

选择 20 3pts

填空 2 3pts

函数 1 8pts

评论