感知机 Perceptron¶
朴素的感知机用于解决二分类问题,是一种线性分类模型,属于判别模型。
输入空间:\mathcal{X}\subset \mathbb{R}^n;输出空间:\mathcal{Y} = \{+1, -1\}。
输入 x\in\mathcal{X} 表示实例的特征向量,对应输入空间(特征空间)中的点;输出 y\in\mathcal{Y} 表示 x 对应的类别。
习题2.2¶
模仿例题2.1,构建从训练数据集中求解感知机模型的例子。
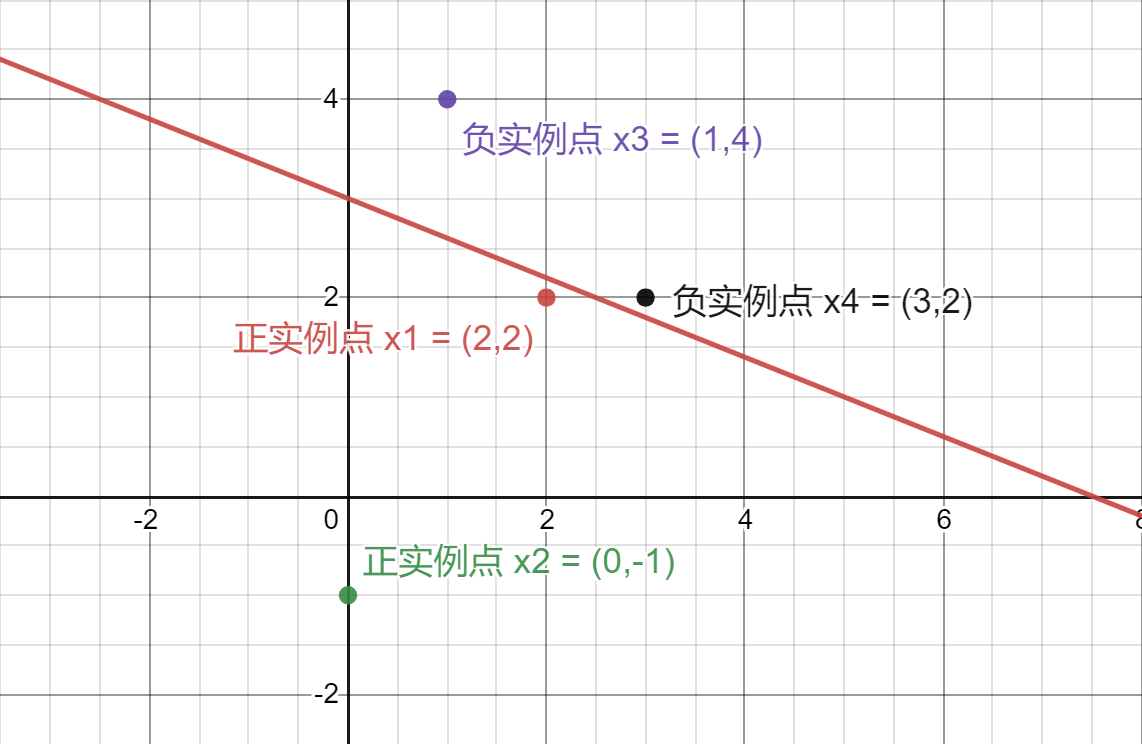
不妨假设某数据集中,正实例点为x_1 = (2, 2)^T, x_2 = (0, -1)^T,负实例点为x_3 = (1, 4)^T, x_4 = (3, 2)^T。现使用感知机学习算法的原始形式求解感知机模型f(x) = {\rm sign}(\omega\cdot x + b),其中\omega = (\omega^{(1)}, \omega^{(2)})^T, x = (x^{(1)}, x^{(2)})^T。
构建最优化问题: $$ \min_{\omega, b}L(\omega, b) = -\sum_{x_i\in M}y_i(\omega\cdot x_i + b) $$ 其中M为误分类点集。
-
取初值\omega_0 = (0, 0)^T, b_0 = 0。取步长\eta = 1。
-
对于x_1 = (2, 2)^T ,y_1(\omega_0\cdot x_1+b_0) = 0 \leq 0,未被正确分类,更新\omega, b $$ \omega_1 = \omega_0 + \eta x_1y_1 = (2, 2)^T, b_1 = b_0 + \eta y_1 = 1 $$ 得到线性模型 $$ \omega_1\cdot x + b_1 = 2x^{(1)} + 2x^{(2)} + 1 $$
-
对于x_1 = (2, 2)^T,y_1(\omega_1\cdot x_1 + b_1) = 9 > 0,被正确分类;
-
对于x_2 = (0, -1)^T,y_2(\omega_1\cdot x_2 + b_1) = -1 \leq 0,未被正确分类,更新\omega, b $$ \omega_2 = \omega_1 + \eta x_2y_2 = (2, 1)^T, b_2 = b_1 + \eta y_2 = 2 $$ 得到线性模型 $$ \omega_2\cdot x + b_2 = 2x^{(1)} + x^{(2)} + 2 $$
-
对于x_1 = (2, 2)^T,y_1(\omega_2\cdot x_1 + b_2) = 8 > 0,被正确分类;
对于x_2 = (0, -1)^T,y_2(\omega_2\cdot x_2 + b_2) = 1 > 0,被正确分类;
对于x_3 = (1, 4)^T,y_3(\omega_2\cdot x_3 + b_2) = -8 \leq 0,未被正确分类,更新\omega, b $$ \omega_3 = \omega_2 + \eta x_3y_3 = (1, -3)^T, b_3 = b_2 + \eta y_3 = 1 $$
得到线性模型 $$ \omega_3\cdot x + b_3 = x^{(1)} - 3x^{(2)} + 1 $$
- 对于x_1 = (2, 2)^T,y_1(\omega_3\cdot x_1 + b_3) = -3 \leq 0,未被正确分类,更新\omega, b
$$ \omega_4 = \omega_3 + \eta x_1y_1 = (3, -1)^T, b_4 = b_3 + \eta y_1 = 2 $$
得到线性模型 $$ \omega_4\cdot x + b_4 = 3x^{(1)} - 1x^{(2)} + 2 $$
- 对于x_1 = (2, 2)^T,y_1(\omega_4\cdot x_1 + b_4) = 6 > 0,被正确分类;
对于x_2 = (0, -1)^T,y_2(\omega_4\cdot x_2 + b_4) = 3 > 0,被正确分类;
对于x_3 = (1, 4)^T,y_3(\omega_4\cdot x_3 + b_4) = -1 \leq 0,未被正确分类,更新\omega, b $$ \omega_5 = \omega_4 + \eta x_3y_3 = (2, -5)^T, b_5 = b_4 + \eta y_3 = 1 $$
得到线性模型 $$ \omega_5\cdot x + b_5 = 2x^{(1)} - 5x^{(2)} + 1 $$
- 循环以上过程,利用代码(下附)算出\omega_{139} = (-2, -5), b_{139} = 15,得到线性模型 $$ \omega_{139}\cdot x + b_{139} = -2x^{(1)} - 5x^{(2)} + 15 $$
对于所有数据点y_i(\omega_{139}\cdot x_i + b_{139})>0,没有误分类点,损失函数达到极小。
分离超平面为:-2x^{(1)} - 5x^{(2)} + 15 = 0
感知机模型为:f(x) = {\rm sign}(-2x^{(1)} - 5x^{(2)} + 15)
习题 2.3¶
证明以下定理:样本集线性可分的充要条件是正实例点集所构成的凸壳与负实例点集所构成的凸壳互不相交。
其中,对于\mathbb{R}^n中点集S = \{x_1, x_2, .., x_k\}的凸壳定义为 $$ {\rm conv}(S) = {x = \sum_{i=1}k\lambda_ix_i:\sum_{i=1}k\lambda_1 = 1, \lambda_i \geq 0, i = 1, 2, .. k} $$
\Longrightarrow:
设正实例点集为S_+,负实例点集为S_-。\forall x_+\in S_+, x_-\in S_-,由线性可分知\omega\cdot x_++b>0,\omega\cdot x_-+b<0。
若两凸壳相交,则\exists x\in{\rm conv}(S_+)\cap{\rm conv}(S_-)。
由x\in {\rm conv}(S_+)知 $$ \omega\cdot x = \sum_{i=1}^k\lambda_i(\omega\cdot x_i)>-\sum_{i=1}^kb\lambda_i=-b $$
由x\in {\rm conv}(S_-)知 $$ \omega\cdot x = \sum_{j=1}^k\lambda_j(\omega\cdot x_j)<-\sum_{j=1}^kb\lambda_j=-b $$
二式矛盾,所以不存在x\in{\rm conv}(S_+)\cap{\rm conv}(S_-),即{\rm conv}(S_+)\cap{\rm conv}(S_-) = \empty。
\Longleftarrow:
由两点集不相交,则存在一超平面将两点集分离,即存在超平面\omega\cdot x + b = 0可以将所有的凸壳中的点进行分离。而显然当\lambda_i=1,\lambda_{j\neq i}=0时,可以取到S_+或S_-中的所有的点x_i。即对于所有的x_i,都可被超平面\omega\cdot x + b = 0线性分离。所以,样本集线性可分。
附 习题2.2所用代码
dot = [(2, 2), (0, -1), (1, 4), (3, 2)]
tag = [1, 1, -1, -1]
eta = 1
omega = [0, 0]
b = 0
cnt = 0
flag = True
while flag:
print('Count %d:' % (cnt))
print(' Omega = (%d, %d), b = %d' % (omega[0], omega[1], b))
flag = False
cnt += 1
for i in range(4):
if tag[i] * (omega[0] * dot[i][0] + omega[1] * dot[i][1] + b) <= 0:
flag = True
omega[0] += eta * tag[i] * dot[i][0]
omega[1] += eta * tag[i] * dot[i][1]
b += eta * tag[i]
break
运行结果:
Count 0:
Omega = (0, 0), b = 0
Count 1:
Omega = (2, 2), b = 1
Count 2:
Omega = (2, 1), b = 2
Count 3:
Omega = (1, -3), b = 1
Count 4:
Omega = (3, -1), b = 2
Count 5:
Omega = (2, -5), b = 1
Count 6:
Omega = (4, -3), b = 2
Count 7:
Omega = (1, -5), b = 1
Count 8:
Omega = (3, -3), b = 2
Count 9:
Omega = (0, -5), b = 1
Count 10:
Omega = (2, -3), b = 2
Count 11:
Omega = (4, -1), b = 3
Count 12:
Omega = (3, -5), b = 2
Count 13:
Omega = (5, -3), b = 3
Count 14:
Omega = (2, -5), b = 2
Count 15:
Omega = (4, -3), b = 3
Count 16:
Omega = (1, -5), b = 2
Count 17:
Omega = (3, -3), b = 3
Count 18:
Omega = (0, -5), b = 2
Count 19:
Omega = (2, -3), b = 3
Count 20:
Omega = (-1, -5), b = 2
Count 21:
Omega = (1, -3), b = 3
Count 22:
Omega = (3, -1), b = 4
Count 23:
Omega = (2, -5), b = 3
Count 24:
Omega = (4, -3), b = 4
Count 25:
Omega = (1, -5), b = 3
Count 26:
Omega = (3, -3), b = 4
Count 27:
Omega = (0, -5), b = 3
Count 28:
Omega = (2, -3), b = 4
Count 29:
Omega = (-1, -5), b = 3
Count 30:
Omega = (1, -3), b = 4
Count 31:
Omega = (3, -1), b = 5
Count 32:
Omega = (2, -5), b = 4
Count 33:
Omega = (4, -3), b = 5
Count 34:
Omega = (1, -5), b = 4
Count 35:
Omega = (3, -3), b = 5
Count 36:
Omega = (0, -5), b = 4
Count 37:
Omega = (2, -3), b = 5
Count 38:
Omega = (-1, -5), b = 4
Count 39:
Omega = (1, -3), b = 5
Count 40:
Omega = (-2, -5), b = 4
Count 41:
Omega = (0, -3), b = 5
Count 42:
Omega = (2, -1), b = 6
Count 43:
Omega = (1, -5), b = 5
Count 44:
Omega = (3, -3), b = 6
Count 45:
Omega = (0, -5), b = 5
Count 46:
Omega = (2, -3), b = 6
Count 47:
Omega = (-1, -5), b = 5
Count 48:
Omega = (1, -3), b = 6
Count 49:
Omega = (-2, -5), b = 5
Count 50:
Omega = (0, -3), b = 6
Count 51:
Omega = (2, -1), b = 7
Count 52:
Omega = (1, -5), b = 6
Count 53:
Omega = (3, -3), b = 7
Count 54:
Omega = (0, -5), b = 6
Count 55:
Omega = (2, -3), b = 7
Count 56:
Omega = (-1, -5), b = 6
Count 57:
Omega = (1, -3), b = 7
Count 58:
Omega = (-2, -5), b = 6
Count 59:
Omega = (0, -3), b = 7
Count 60:
Omega = (-3, -5), b = 6
Count 61:
Omega = (-1, -3), b = 7
Count 62:
Omega = (1, -1), b = 8
Count 63:
Omega = (0, -5), b = 7
Count 64:
Omega = (2, -3), b = 8
Count 65:
Omega = (-1, -5), b = 7
Count 66:
Omega = (1, -3), b = 8
Count 67:
Omega = (-2, -5), b = 7
Count 68:
Omega = (0, -3), b = 8
Count 69:
Omega = (-3, -5), b = 7
Count 70:
Omega = (-1, -3), b = 8
Count 71:
Omega = (1, -1), b = 9
Count 72:
Omega = (0, -5), b = 8
Count 73:
Omega = (2, -3), b = 9
Count 74:
Omega = (-1, -5), b = 8
Count 75:
Omega = (1, -3), b = 9
Count 76:
Omega = (-2, -5), b = 8
Count 77:
Omega = (0, -3), b = 9
Count 78:
Omega = (-3, -5), b = 8
Count 79:
Omega = (-1, -3), b = 9
Count 80:
Omega = (-4, -5), b = 8
Count 81:
Omega = (-2, -3), b = 9
Count 82:
Omega = (0, -1), b = 10
Count 83:
Omega = (-1, -5), b = 9
Count 84:
Omega = (1, -3), b = 10
Count 85:
Omega = (-2, -5), b = 9
Count 86:
Omega = (0, -3), b = 10
Count 87:
Omega = (-3, -5), b = 9
Count 88:
Omega = (-1, -3), b = 10
Count 89:
Omega = (-4, -5), b = 9
Count 90:
Omega = (-2, -3), b = 10
Count 91:
Omega = (0, -1), b = 11
Count 92:
Omega = (-1, -5), b = 10
Count 93:
Omega = (1, -3), b = 11
Count 94:
Omega = (0, -7), b = 10
Count 95:
Omega = (2, -5), b = 11
Count 96:
Omega = (-1, -7), b = 10
Count 97:
Omega = (1, -5), b = 11
Count 98:
Omega = (-2, -7), b = 10
Count 99:
Omega = (0, -5), b = 11
Count 100:
Omega = (-3, -7), b = 10
Count 101:
Omega = (-1, -5), b = 11
Count 102:
Omega = (1, -3), b = 12
Count 103:
Omega = (0, -7), b = 11
Count 104:
Omega = (2, -5), b = 12
Count 105:
Omega = (-1, -7), b = 11
Count 106:
Omega = (1, -5), b = 12
Count 107:
Omega = (-2, -7), b = 11
Count 108:
Omega = (0, -5), b = 12
Count 109:
Omega = (-3, -7), b = 11
Count 110:
Omega = (-1, -5), b = 12
Count 111:
Omega = (1, -3), b = 13
Count 112:
Omega = (0, -7), b = 12
Count 113:
Omega = (2, -5), b = 13
Count 114:
Omega = (-1, -7), b = 12
Count 115:
Omega = (1, -5), b = 13
Count 116:
Omega = (-2, -7), b = 12
Count 117:
Omega = (0, -5), b = 13
Count 118:
Omega = (-3, -7), b = 12
Count 119:
Omega = (-1, -5), b = 13
Count 120:
Omega = (-4, -7), b = 12
Count 121:
Omega = (-2, -5), b = 13
Count 122:
Omega = (0, -3), b = 14
Count 123:
Omega = (-1, -7), b = 13
Count 124:
Omega = (1, -5), b = 14
Count 125:
Omega = (-2, -7), b = 13
Count 126:
Omega = (0, -5), b = 14
Count 127:
Omega = (-3, -7), b = 13
Count 128:
Omega = (-1, -5), b = 14
Count 129:
Omega = (-4, -7), b = 13
Count 130:
Omega = (-2, -5), b = 14
Count 131:
Omega = (0, -3), b = 15
Count 132:
Omega = (-1, -7), b = 14
Count 133:
Omega = (1, -5), b = 15
Count 134:
Omega = (-2, -7), b = 14
Count 135:
Omega = (0, -5), b = 15
Count 136:
Omega = (-3, -7), b = 14
Count 137:
Omega = (-1, -5), b = 15
Count 138:
Omega = (-4, -7), b = 14
Count 139:
Omega = (-2, -5), b = 15