Digital Logic

Introduction

Every problem in computer science can be solved by adding another level of indirection.

对于解决不了的问题，可以多加一层来解决。

System

操作系统 - Operating System

体系结构 - ISA 位指令集结构 Instruction Set Architecture

计算机组成 - Computer Organization

数字逻辑电路 - Register Transfer Level, Digital Logic Circuit

系统Ⅰ：简单指令(单周期CPU) -> 简单指令(流水线) -> 基本指令 + kernel

冯诺伊曼架构 数据和指令混在一起不区分

存储数据

0: Zero Voltage(电压), 1: Positive Voltage，物理实现中，是在某一范围波动都认为是某一值

bit: smallest unit of information 0/1

CPU

Arithmetic and Logic Unit 算术和逻辑运算单元；Control Unit 控制单元；寄存器(包括program counter 当前指令的下一条地址, current instruction 当前指令)

课程相关

数字逻辑与计算机组成 袁春风、武港山等 机械工业出版社

Computer Organization and Design, RISC-V Edition, 1^st Edition

参考：CSAPP 深入理解计算机系统

实验不分组

成绩

期末 30% + 7 Labs 55% + 作业 10%

Lab Bonus 10%

迟交一天，扣 5%

Computer System and Information Representation

Introduction to Computer System

CPU：控制部件、Data Pass 数据总线（很多设备共享同一条线，达到更高利用率）

控制部件（一些寄存器）：

• MAR: Memory Address Register 向内存中写数据

• MDR: Memory Data Register 从内存中读写数据

• PC: Program Counter 当前指令的下一条地址

• IR: 当前指令

把高级语言变成机器型语言：

Translator: Assembler, Interpreter, Compiler

Interpreter: 解释器，把程序变成字节码之后，由解释器运行（平台无关）

Compiler: 编译器，把程序变成某个CPU/系统可以直接运行的机器码（平台相关）

5阶段：

Instruction Fetch -> Instruction Decode -> Execute -> Memory Access -> Write Back

一般采用流水线的方式，第一阶段干完了不会等着最后一个干完，而是马上开始干下一个任务

Binary number representation

二进制表示

模拟电路（Analog），数字电路（Digital）

数字电路中又分为异步（Asynchronous）时间连续、值离散；同步（Synchronous）时间离散、值离散，一般使用异步数字电路和一个时间信号做与/或运算得到

高电平代表1，低电平代表0，中间有一部分电平代表无效区间

计数系统 Carry Counting System

基：Radix，十进制与二进制浮点数的数学表示 $$ 3A.C\Leftrightarrow3\times16^1+ 10\times 16^0 + 12\times 16^{-1} = 58.75 $$ 短除法 整数部分，十进制转二进制

连乘法 小数部分。十进制转二进制 $$ 0.65\times 2 = \mathbf{1}.3\ 0.3\times 2 = \mathbf{0}.6\ 0.6\times 2 = \mathbf{1}.2\ 0.2\times 2 = \mathbf{0}.4\ 0.4\times 2 = \mathbf{0}.8\ 0.8\times 2 = \mathbf{1}.6\ \cdots $$ 四进制/八进制/十六进制 直接并排写出即可

Arithmetic operation

Z means the carry/borrow flag before this calc.

Single Bit Binary Addition with Carry: List every conditions, C means carry flag

Single Bit Binary Subtraction with Borrow: B means borrow flag

Binary Multiplication, Division

Representation of numeric data

三要素：进位系统、数字表示（定点数 Fixed-point Number、浮点数 Float-point Number）、编码方法

Fixed-Point Number Representation

PPT 中的 两个概念？

假设有 $n$ 位，对于无符号整型：最大到 $2^n - 1$；对于有符号整型：取决于 Encoding Methods

Encoding Methods

原码 Original Code 补码 Complement Code 反码 Inverse Code 转码 Frameshift Code

Original Code - Sign and Magnitude Representation

符号位 + 数值位：绝对值相同的数，后 $n - 1$ 位相同，只有第 $1$ 位不同。

问题：$+0\neq -0$，有两种表达 $0$ 的方式，导致不能仅凭符号位判定正负，而且运算时符号位和数值位要分开处理。

Complement Code - 2's complement

仍然使用符号位，但对于数值位使用同余的关系，在同余系（$n-1$ 个 Bit 的数值位系统，Modulo 为 $2^{n-1}$）内做运算：把溢出部分丢掉，把负数全部替换为对应的非负数 $$ [X_T]_C = 2^n + X_T(-2^{n-1}\leq X_T<2^{n-1}, \mod 2^n) $$ 小问题：Overflow, 且之后后 $n$ 位才能表示实际的计算结果，$n+1$ 或更高位无法表示真实计算结果。

为什么 $X_T<2^{n-1}$： $$ \begin{aligned}[] [2^{n-1}]_C &= 2^n + 2^{n - 1} \mod{2^n} \ &= 2^{n-1}\ \end{aligned} $$

$$\begin{aligned}[] [-2^{n-1}]_C &= 2^n - 2^{n - 1} \mod{2^n} \\ &= 2^{n-1}\\ \end{aligned}$$

运算 Shortcut：对于负数，取反加一；如果需要将少位扩展为多位，只需要把原来的符号位复制到新位，即 $$ (1001)\rightarrow (1111 1001) $$

Inverse Code - 1's complement

主要问题：无法快速解决循环借位：End-around carry/borrow

Frameshift Code

符号位 + 幂次 + 小数点后的位

最终补码脱颖而出。补码在存储中，有无符号的存储方式是一致的，只是在解释 (Interpret) 时会赋予它特定含义。

在 C 里，不要将无符号整型和有符号整型直接比较，因为 C90 标准里是视作无符号整型比较的，C99 标准中是视作有符号整型比较的。

C 中的位运算

x = x ^ y;
y = x ^ y;
x = x ^ y;

右移分为逻辑右移（针对无符号数，补0），算数右移（针对有符号数，补符号位）

补码运算时的统一性 $$ B2U = \sum_{i = 0}^{w-1}x_i\times 2^i, B2T = -x_{w-1}\times 2^{{w-1}+\sum_{i=0}}{w-2}x_i\times 2^i $$ 有符号的运算，和无符号的运算，过程和结果在机器码层面是一致的。

C 语言中数据最值

// #include <limits.h>, All platform the SAME
#define INT_MAX 2147483647
#define INT_MIN (-INT_MAX-1)
#define UINT_MAX 0xffffffff
// Values platform specific, e.g. x64 LONG_MAX = 2^63 - 1
#define ULONG_MAX
#define LONG_MAX
#define LONG_MIN (-LONG_MAX-1)

符号型与非符号型的转换 $$ u_x = \begin{cases} s_x, & x\geq 0\ s_x + 2^n, & x \lt 0\ \end{cases} $$

当 $s_x\gt 0$ 时，可以通过减法计算取负：

$$-s_x = 0 - s_x = 2^n - s_x$$

C 语言中，当无符号类型和有符号类型进行大小比较时，将它们转化为无符号类型再进行比较。

信息泄露攻击

/* Kernel memory region holding user accessible data */
#define KSIZE 1024
char kbuf[KSIZE];

/* Copy at most maxlen bytes from kernel region to user buffer */
int copy_from_kernel(void user_dest , int maxlen)
    /* Byte count len is minimum of buffer size and maxlen*/
    int len = KSIZE < maxlen ? KSIZE : maxlen;
    memcpy(user_dest, kbuf, len);
    return len;
}

/* Declaration of library function memcpy */
/* void *memcpy(void *dest, void *src, size_t n); */

memcpy 的第三参数是 size_t，是无符号的。如果传入的 maxlen < 0，会导致远远多于 KSIZE 的数据被泄露到 user_dest 中。

怎样解决？

符号扩展 Sign Extension

对于符号数，把 $w$ 位补为 $w+k$ 位：后 $w$ 位不动，前 $k$ 位补符号位。

Signed Truncating ???

有符号加法和无符号加法都可以构成阿贝尔群，且有转化：

乘法

-128 * -1 = -128

对未分配的内存存入数据

void* copy_elements(void ele_src [], int ele_cnt , size_t ele_size) {
    /*
    * Allocate buffer for ele_cnt objects, each of ele_size bytes
    * and copy from locations designated by ele_src
    */
    void *result = malloc(ele_cnt * ele_size);
    if (result == NULL)
        /* malloc failed */
        return NULL;
    void *next = result;
    int i;
    for (i = 0; i < ele_cnt; i++) {
        /* Copy object i to destination */
        memcpy(next, ele_src[i], ele_size); 
        /* Move pointer to next memory region */
        next += ele_size;
    }
    return result;
}

只用 malloc 分配了 ele_cnt * ele_size % 2^32 的空间，但是逐次使用了 ele_cnt * ele_size 的空间。

乘法位运算

(u << 5) - (u << 3) $\Leftrightarrow$ u * 24

除法 $$ x = qy + r, 0\leq r < y\ \frac{x+y-1}{y} = q + (r + y - 1)/y\ \lfloor\frac{x+y-1}{y}\rfloor = q + \lfloor(r + y - 1)/y\rfloor $$ 再看，除法使用右移来计算，由此产生的偏差用取整来弥补

和算术运算都是环，但是不满足 $u>0\Rightarrow u+v>v$，$u>0,v>0\Rightarrow uv>0$

为什么要用无符号？

需要用作边界条件的时候不要用无符号

for (int i = cnt; i - sizeof(int) >= 0; i -= sizeof(int));

会停不下来的。

多精度问题时/位操作时，需要使用无符号

浮点数

二进制的性质决定它会使用很多无限循环小数来表达很多十进制中常见的有理数。

如果直接固定小数点的位置，整数部分小数部分分别转换成二进制进行存储，会出现浪费

IEEE Standard 754 $$ (-1)^s \times M \times 2^E $$ 32位，符号 s 1 位，exp 8 位，frac 23 位

64位，符号 s 1 位，exp 11 位，frac 52 位

80位，符号 s 1 位，exp 位，frac 位（Intel CPU）

$M$ 和 $E$ 不直接对应，但是是有对应关系的

$E$ 会加上一个 Bias，一般是 $2^{k-1}-1$，如 32 位的阶码位数为 8，$2^7-1 = 127$。$E = \exp - Bias$。

为什么IEEE编码要减 1？为了使用阶码为 0 的情形来表示 0 附近的数，为了使用阶码全是 1 的情形来表示无穷大和 NaN（Not A Number，在这种情形下一般的计算是不成立的）。

$M\in [1,2)$ 会把最前面的 "$1.$" 去掉。

由于如果只使用上面的规则，没有办法很好的处理 0 的问题，以至于在 0 附近出现很大的 Gap：最小只能是 $1\times 2^{-126}$，它和 0 直接相差 $2^{-126}$，但是比他大的那个数是 $(1+2^{-23})\times 3^{-126}$，距离只有 $2^{-149}$，这会导致两边距离差距太大，所以要引入特殊情形 Denormalized Values。

0 附近的（exp = 0）：

仍然使用 $2^{1-Bias}=2^{-126}$ 的阶，但是把 $M$ 的 $1.$ 变为 $0.$，此时的 $E\neq 0-Bias$，而是 $E = 1-Bias$。

frac = 0时，都是 0。会产生 $+0$ 和 $-0$ 的问题，要额外考虑。

无穷/NaN（exp 全是 1）：

当 frac = 0 时，表示无穷，当 frac ≠ 0 时，表示 NaN。

nan 在逻辑表达式中，得到的全都是 False。存储中，它比任何数都大。

分为两种，Quiet NaN（不会异常），Signaling NaN（会发生异常）

运算

首先计算精确值，再存入期望的精度：frac 左移/右移，对应 exp +1/-1

exp 过长时，会产生溢出

frac 过长时，需要取整：如果取证位后面是 10000，那就在取证位上取**最近的偶数**，具有更好的统计效果。

乘法时，符号位异或，主要的麻烦在于 $M_1\times M_2$

加法时，首先计算精确值，再存入期望的精度

这样定义的加法不是阿贝尔群：（乘法也不是环，类似）

• 不封闭（可能产生 inf 或 NaN）

• 可交换

• 不满足结合律（$(a+b)+c\neq a+(b+c)$），比如 $(3.14+1^{-10})-1^{-10}$ 可能不是 $3.14$，因为可能会 Round；但是 $3.14+(1^{-10}-1^{-10})$ 一定是 $3.14$。

• 有零元，但是 inf 和 nan 没有逆元

• 单调性 $a\geq b\Rightarrow a+c\geq b+c$，但是对 inf 和 nan 不成立

Multiplication distributes over addition? Possibility of overflow, inexactness of rounding

比较 C 中是否有精度损失：

int 精度比 float 中的 M 的位数要多，所以会损失

Binary Codes for Decimal Digits

用二进制表达十进制数，BCD: Binary Coded Decimal

Weight BCD Code (common used: 8421 code), No weight BCD Code (Gray code, Excess3 code 余3码)

Excess3 Code: 在 8421 基础上加 3（0 用 0011 表示）

格林码：相邻数字之间只有一个 bit 不一样

Representation of non numeric data, data width and storage

bits / characters

American Standard Code for Information Interchange: 7 bits

32 位系统中，int, long 都是 4 位；64 位系统中，long 是 8 位。

Least Significant Bit vs. Least Significant Byte 最低位/最低 Byte

Big Endian: Least Significant Byte has highest address; Little Endian

Foundations of Digital Logic

Introduction

输入时模拟信号到数字信号，数字信号处理，再转换为模拟信号输出

模拟信号只有一些经验表达式，没有太多公式推导

Binary Logic and Gates

逻辑运算：AND($\cdot$), OR($+$), NOT($\bar{A}, A', \sim A$), XOR($\oplus$)

一些符号，元件图

inversion (NOT), buffer(0 通过之后就是 0，1 通过之后就是 1), AND, OR, XOR, NAND, NOR, XNOR.

Digital abstraction

GND Ground 接地，电压为 0。

$V_{CC}$ 源电压（CMOS 中也会用 $V_{DD}/V_{SS}$，一般5V）

$V_{IH}, V_{IL}, V_{OH}, V_{OL}$ 逻辑电平，代表哪些电压范围代表1，哪些电压状态代表0

由于输出后，在传输过程中会有损耗，所以 $V_{IH} = V_{OH} - NM_{H}$，这里的 $NM_{H}$ 是我们可以容忍的噪声的限度，指噪声对信号产生的最大影响

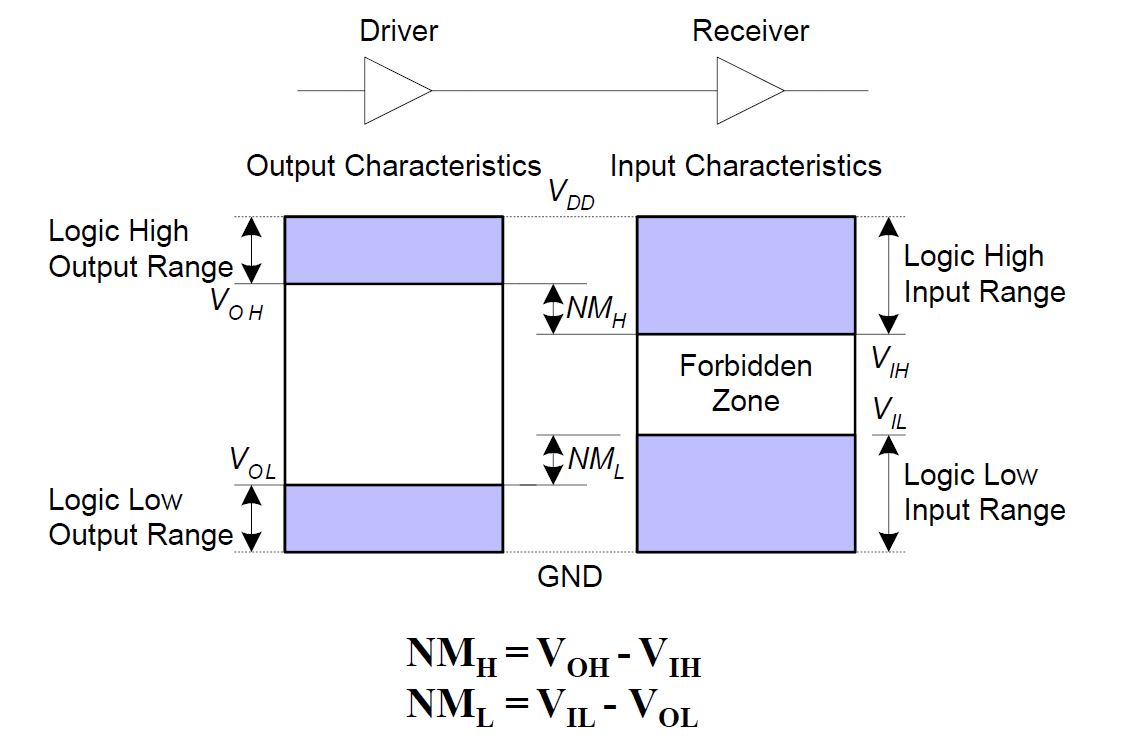
选取时，取斜率为1的点进行测量？

Transistors 晶体管

早期 TTL 功耗大

CMOS 整体架构：gate 栅极 source 源极 drain 漏极，具体可以分为 2 类 - nMOS, pMOS

nMOS 可以保证 gate 输入是 0 的时候，无论 source 是什么，drain 输出都是 0（不通）；但是 gate 输入是 1 的时候，得到的 drain 是被削弱的了 source。

pMOS 可以保证 gate 输入是 1 的时候，不通；但是 gate 输入是 0 时，通。（传 1 不会削弱，传 0 会削弱）

所以，nMOS 接地，pMOS 接电源。

非门：

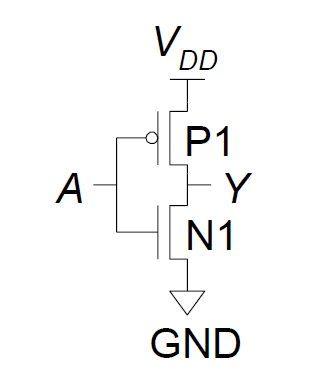
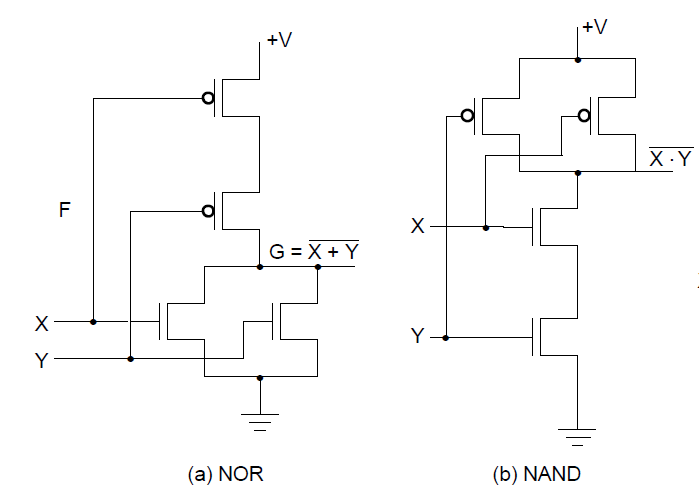
一般的多输入的门：一个 MOS 串联，一个 MOS 并联

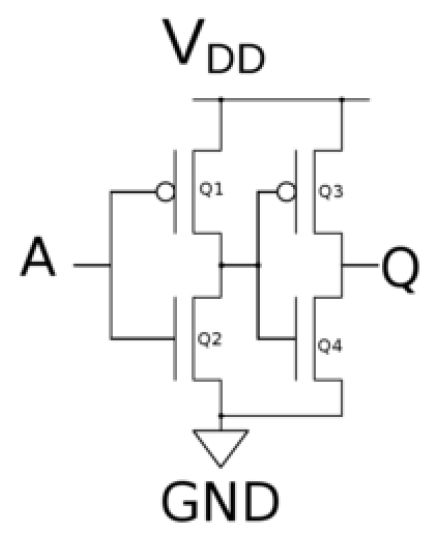
Buffer 相当于两个非门相连，可以创造延迟

Transmission Gate

A 是高电平，所以两个晶体管都导通；IN 为 1 时，主要由 pMOS 起作用，IN 为 0 时 主要由 nMOS 起作用。高阻值状态：Z。

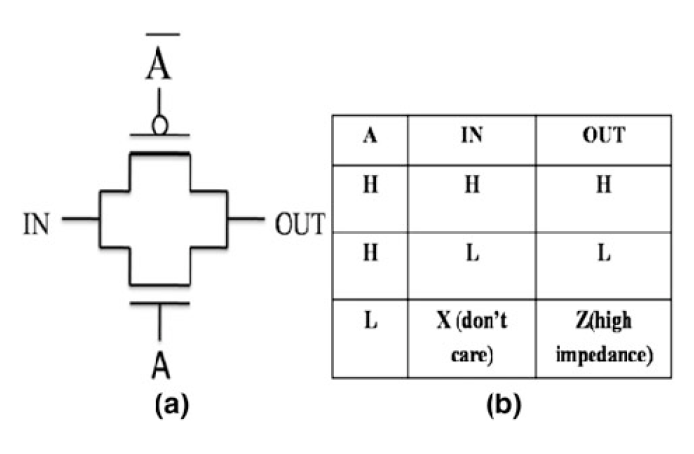
Propagation delay (tpd)

在电路传输过程中，可能出现一些延迟。

当从 input 电平变化时开始计起，output 显现从 output 的高电平到低电平的变化所需的时间为 $t_{\text{PHL}}$；当从 input 电平变化时计起，output 显现这个从 output 的低电平到高电平的变化所需的时间为 $t_\text{PLH}$。

一般来讲传输的电压和延时是负相关的，但是如果电压高了功耗又高了。

Rise and Fall Time ($T_r$ , $T_f$)

对于信号而言，也需要时间去达到输出的电平，分别记从低到高为 $t_r$，从高到低为 $t_f$

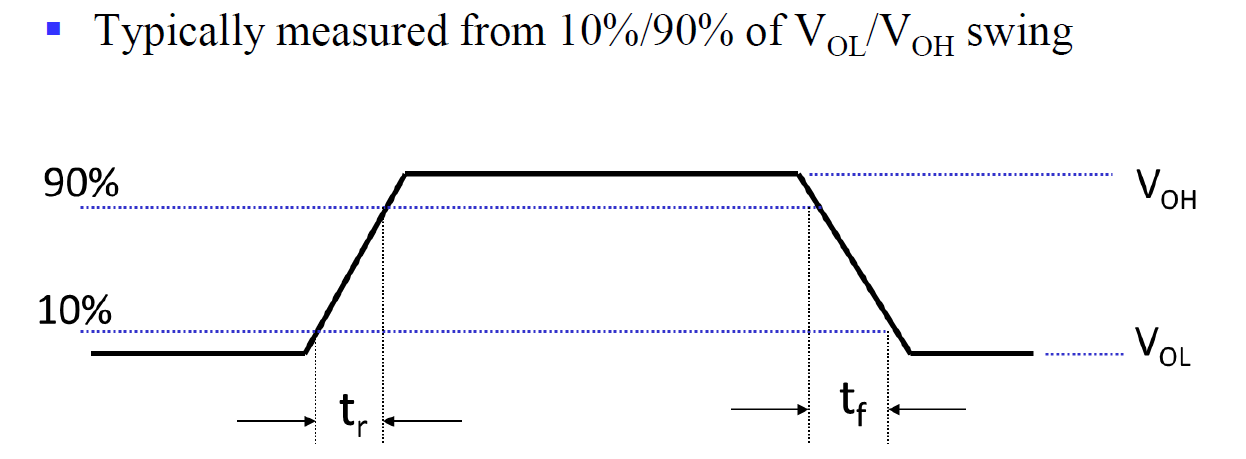
Power dissipation

功率损耗

静态功率损耗：由于泄露的电流而产生的功率损耗 $P_s = I_{DD}V_{CC}$，对于 CMOS 而言很小。

动态功率损耗：由于状态改变，会充放电，不可避免的有功耗损耗

$C_{PD}$ 信号变化时电能的功率损耗

$C_L$ 用来驱动其他设备的负载电容

$f$ 0.5倍的每秒输出变化频次

$P_D = (C_{PD} + C_L)\times V_{CC}^2\times f$

Fan in and Fan out

对于一个晶体管，几个输入能驱动几个输出是有上界的。

Boolean Algebra

布尔代数不只是 Switching Algebra（二值逻辑），可以是多值的

我们只研究 Switching Algebra 中的两阶段逻辑：Two Level Logic

公理及定理：

5条公理及其5条对偶（and 换成 or，01互换）

5条单变量定理及其4条对偶

6条多变量定理及其6条对偶

T8D: $X + YZ = (X + Y)(X + Z)$，或的两边出现互为取反的表达式时，可以消掉一个

T9/T9D: $X + XY = X$, $X(X + Y) = X$，可以去掉某个变量，消除冗余项

T11: $XY + \overline{X}Z+ YZ= XY + \overline{X}Z$，消除冗余项

T11D: $(X + Y)(\overline{X} + Z)(Y + Z) = (X + Y)(\overline{X} + Z)$，消除冗余项

4条n变量定理及其3条对偶

T13, T13D 是德摩根律一般形态，T14 是其推广并抽象化，证明： $$ X+Y + \overline{X}\cdot\overline{Y} = (X+Y+\overline{X})(X+Y+\overline{Y}) = (1+X)(1+Y) = 1\ (X+Y)(\overline{X}\cdot\overline{Y}) = 0\cdot \overline{Y} + 0\cdot\overline{X} = 0 $$

T15, T15D 香农定理：可以减少输入，类似条件概率

T15D 为什么对？ $$ F(X_1, \cdots, X_n) = X_1F(1,\cdots, X_n)+\overline{X}_1F(0,\cdots, X_n) $$

$$F(X_1, \cdots, X_n) = [X_1+F(1,\cdots, X_n)][\overline{X}_1+F(0,\cdots, X_n)]$$

优先级：括号、NOT、AND、OR

对偶：

and 换成 or，01互换，不会互换取反；即使是有 and or 在取反号里，也是简单的互换

自对偶：自己的对偶还是自己

一个等式，可以左右同时取对偶，等式依然成立 $$ \overline{X}\overline{Y}Z+X\overline{Y} = \overline{Y}(X+\overline{X}Z)\xlongequal{\text{T8D}}\overline{Y}(X+\overline{X})(X+Z) = \overline{Y}(X + Z) $$

Logic functions

真值表：假定哪个是 1 哪个是 0（if, if, if, ...），实在不行的时候可以利用真值表证明相等

布尔表达式不是唯一的，但是真值表是唯一的

函数的取反：对偶 + 变量也取反

布尔表达式的**规范型** Canonical Forms

minterm: 每个变量严格只出现一次的乘项

maxterm: 每个变量严格只出现一次的加项

每一个最小项都可以对应一个二进制数，$\overline{X}YZ=011$，这相当依次在真值表中读取一种变量 01 排列；

每一个最大项也可以对应一个二进制数，$X+\overline{Y}+\overline{Z}=011$。

规范型：唯一的最小项之和（最小项全部加起来得到的是1），或是唯一的最大项之积（最大项全部乘起来是0）

可以由真值表，直接确定规范型

布尔表达式的**标准型** Standard Forms

规范型中要求每一个最小项/最大项中，每个变量都出现，所以可能有冗余，标准型中去掉了这种冗余。标准型也是不唯一的。

把标准型化为规范型：补 1 或补 0。 $$ \begin{aligned} f(x,y,z) &= \overline{x}\overline{y}z + y\overline{z} + x\overline{z}\ &= \overline{x}\overline{y}z + (x+\overline{x})y\overline{z} + x\overline{z}\ \end{aligned} $$ $$ \begin{aligned} F(X,Y,Z) &= \sum m(1,2,4,6)\ &= \sum m(001, 010, 100, 110)\ &= \overline{X}\overline{Y}Z + \overline{X}Y\overline{Z} + X\overline{Y}\overline{Z} + XY\overline{Z} \end{aligned} $$

使用 maxterm 时，$F = \prod M(0,3,5,7)$

Circuit Optimization

Literal cost (L)

数数变量出现多少个，下例中 L=8 $$ BD+A\overline{B}C+A\overline{C}\overline{D} $$ Gate input cost (G)

不管最外层的与门/或门，只是在 Literal Cost 的基础上加上项数，下例中 L=9, G=12 $$ BD+A\overline{B}C+A\overline{C}\overline{D}+C $$ Gate input cost with NOTs (GN)

再加上 Not，下例中 L = 10, G = 14, GN = 17 $$ (A+B)(A+D)(B+C+\overline{D})(\overline{B}+\overline{C}+D) $$

Simplification of logic functions

Algebra Method, Use the theorems;

Karnaugh Map, Graphical representations

使用类似格雷码的编码，相邻格子之间只有一位不同，原理：$AB+A\overline{B} = A$

一般超过 4 个就不再使用，用法就是画最大的圈圈，最小值的话就是把圈里的加起来，这样就化简很多。画圈圈一般画 2 的倍数（因为是 prime 的），不要忘记考虑边界和四个角也是可以拼起来的。

蕴含项 Implicant: Product of literals ABC, AC, BC, 每一种可能的圈，圈的大小是 $2^n$。

Prime Implicant: implicant corresponding to the largest circle in a K map, i.e., is a product term obtained by combining the maximum possible number of adjacent squares in the map into a rectangle with the number of squares a power of 2. 没有其他更大的蕴含项可以 Cover 它的蕴含项。

Essential Prime Implicant: A prime implicant is called an Essential Prime Implicant if it is the only prime implicant that covers (includes) one or more minterms. 必须含有至少一个没被包含在其它蕴含项中的项，而且它一定得也是 PI。

找质蕴含项（PI）：

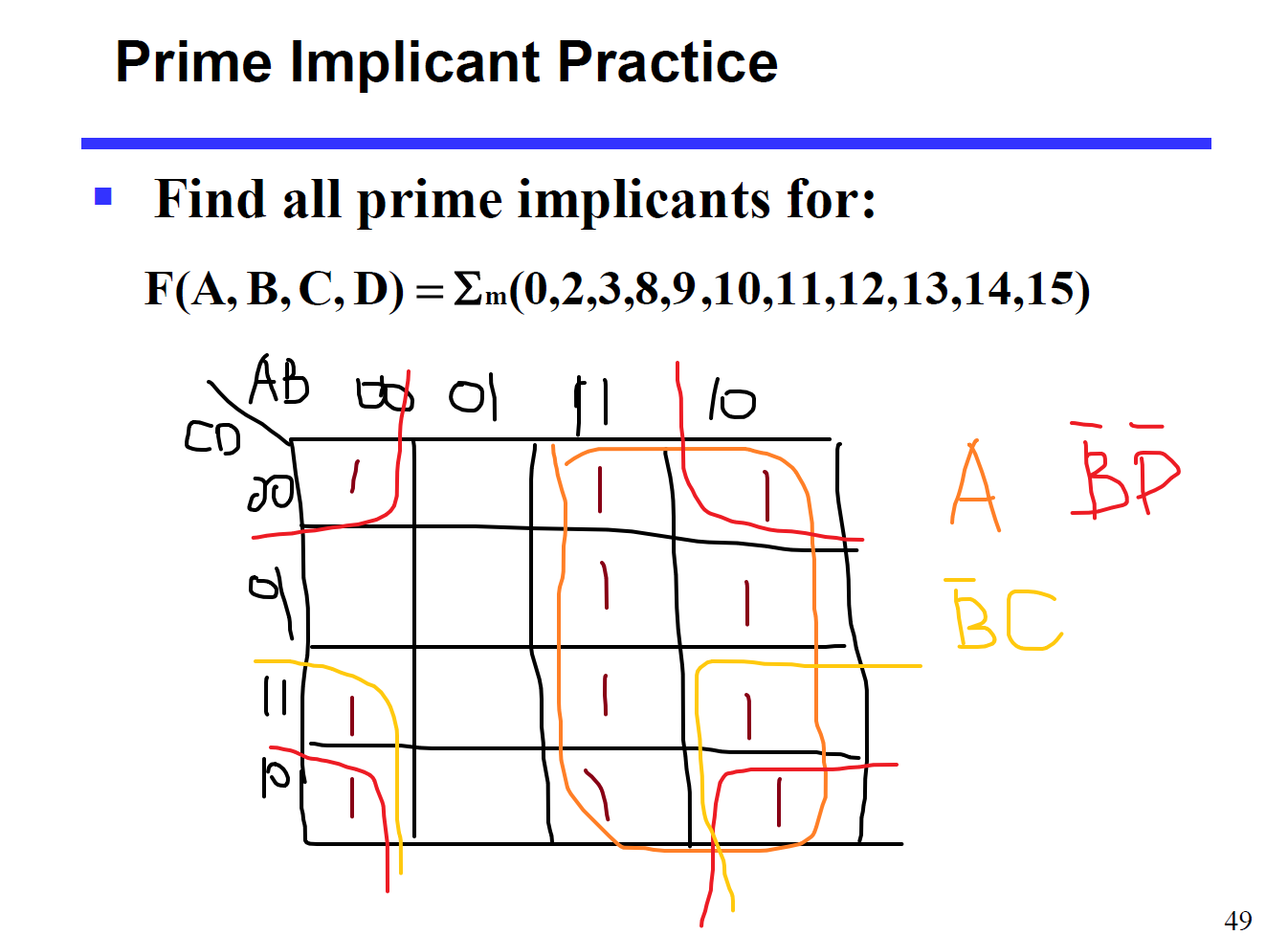$$ F(A,B,C,D) = A+\overline{B}\overline{D}+\overline{B}C $$ 找实质蕴含项（EPI），然后再找一些 Selected PI 覆盖所有的项：

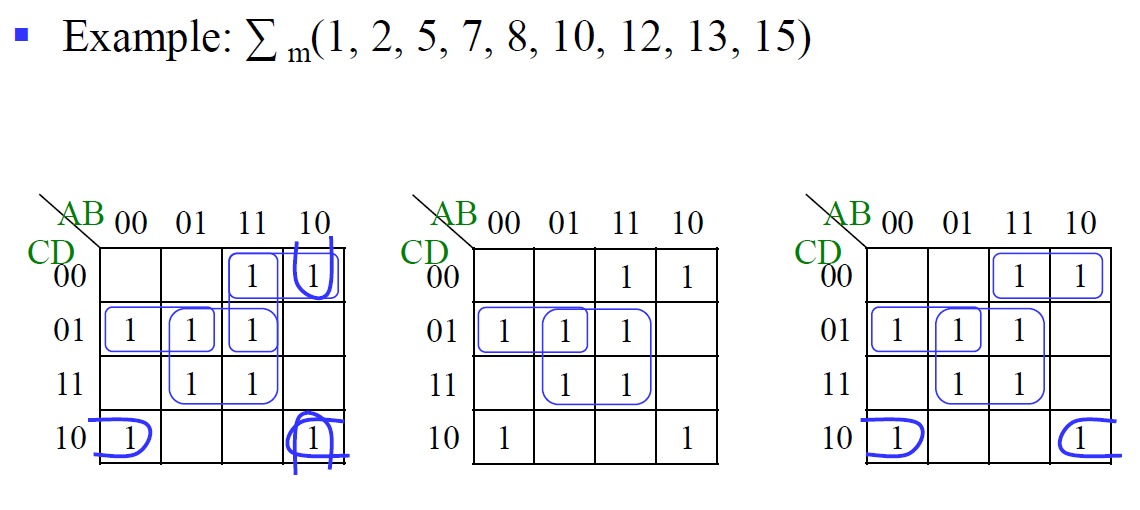
先把那些所有项都被其他质蕴含项 Cover 的去掉，得到图2，然后再把那些没被 Cover 的质蕴含项加回去作为 Selected PI。

如果有 don't case 的项 x，可以把它当成 1 来看，但是不额外加 Selected PI。即，如果加上他可以让 4 个变 8 个，就加，要不然丢在外面也可以。

De Morgan's Theorem in Circuit

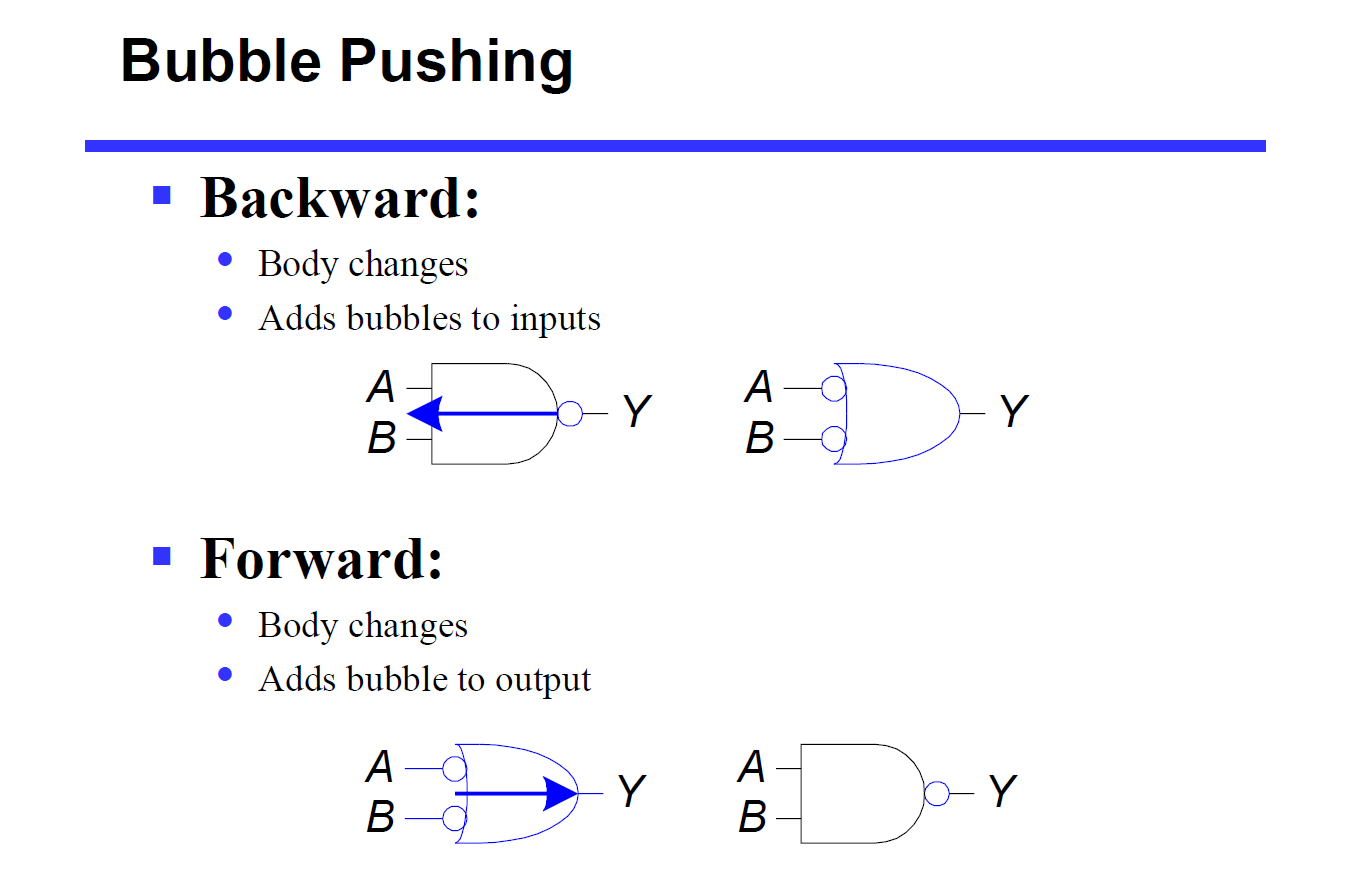
Combinational Logic Design

Introduction to Verilog HDL

FPGA, ASIC(专用集成电路) 硬件描述语言，并非类似 CPU, GPU 的软硬件分开

CPU 等通过指令操作硬件，增加了通用性但是牺牲了效率。

HDL: Hardware description language

设计流程：Logic design with HDL, Simulation, Synthesis 形成逻辑电路上的整合, Physical Design 物理设计（布局、布线、静态时序分析 Delay）, Final step 流片

Modeling methods

Structured Modeling: Module level, Gate level, Switch level

Dataflow Modeling: 数据在电路中流动的方向，组合逻辑电路

一般设计 Gate Level 编程的方法：画真值表，然后简化表达，然后画图

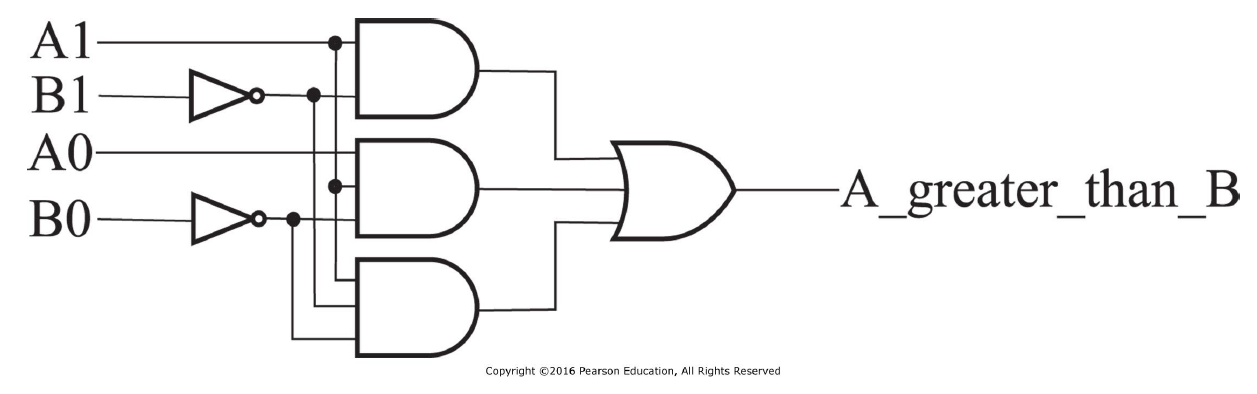
门级：

数据流：

条件：

行为级（可能出现不了解的错误）：

About combinational logic circuits

数字逻辑电路，可以理解成一些输入 -> 一些输出

组合 Combinational 逻辑电路：当前输出只取决于当前输入

时序 Sequential 逻辑电路：结果由当前输入和以前的状态共同决定

性质：

• 每个 Element 都可以表达成一个组合逻辑电路

• Node 节点：指的是线相交的地方，它只能作为一个 Element 的输出

• 组合逻辑电路中不能有回路 Loop

Design Choice：

理论上来讲，所有逻辑电路都可以通过规范型，来形成一个只有 2 层的电路，例如，若使用 minterm，第一层全是 AND，第二层是一个大 OR。有时候某个门的输入太多，所以实际上还是需要使用多级电路 Multi-Level。

Some classic/basic designs

Encoder and decoder

多路选择器 Multiplexer

对应的布尔表达式： $$ F = \overline{S_0}\overline{S_0}A + \overline{S_0}S_1B + S_0\overline{S_1}C + S_0S_1D $$ 如果拆分成 Decoder 和 AND-OR，相当于上式加括号，可以减小复杂度，而且更清晰。

多路分配器 Demultiplexer

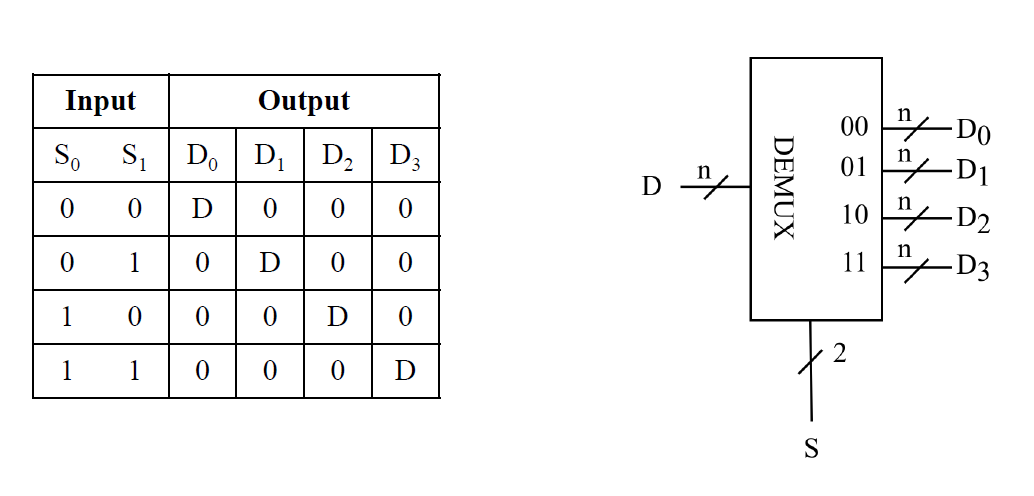
D 只能出现在 D1, D2, D3, D4 中的一个

把多个输入端输入到总线上，再在输出时从主线通过分配器分配信号

半加器 Half Adder

不考虑进位输入

$$ F = A\oplus B, C_{out} = AB $$ 全加器 Full Adder

只需要按照真值表，把指为 1 的加起来： $$ \begin{aligned} F &= \overline{A}\overline{B}C_{in}+ \overline{A}B\overline{C_{in}}+ A\overline{B}\overline{C_{in}} + ABC_{in}\ &\xlongequal{\triangle}A\oplus B\oplus C_{in}\ \end{aligned} $$ 异或运算中，取 1 的变量值个数是奇数。 $$ \begin{aligned} C_{out} &= \overline{A}BC_{in} + A\overline{B}C_{in} + AB\overline{C_{in}} + ABC_{in}\ &= BC_{in} + A\overline{B}C_{in} + AB\overline{C_{in}}\ &= (B + A\overline{B})C_{in} + AB\overline{C_{in}}\ &= (B + A)(B + \overline{B})C_{in} + AB\overline{C_{in}}\ &= AC_{in} + BC_{in} + AB\overline{C_{in}}\ &= A(C_{in} + B\overline{C_{in}}) + BC_{in}\ &= A(B + C_{in}) + BC_{in}\ &= AB + (A + B)C_{in}\ \end{aligned} $$ 如果一个变量和它的取反同时出现在加号两边，可以使用 T8D。

利用半加器实现全加器：一种画法清晰的方法 - 对于进位使用全加器，对于这一位的输出使用半加器。

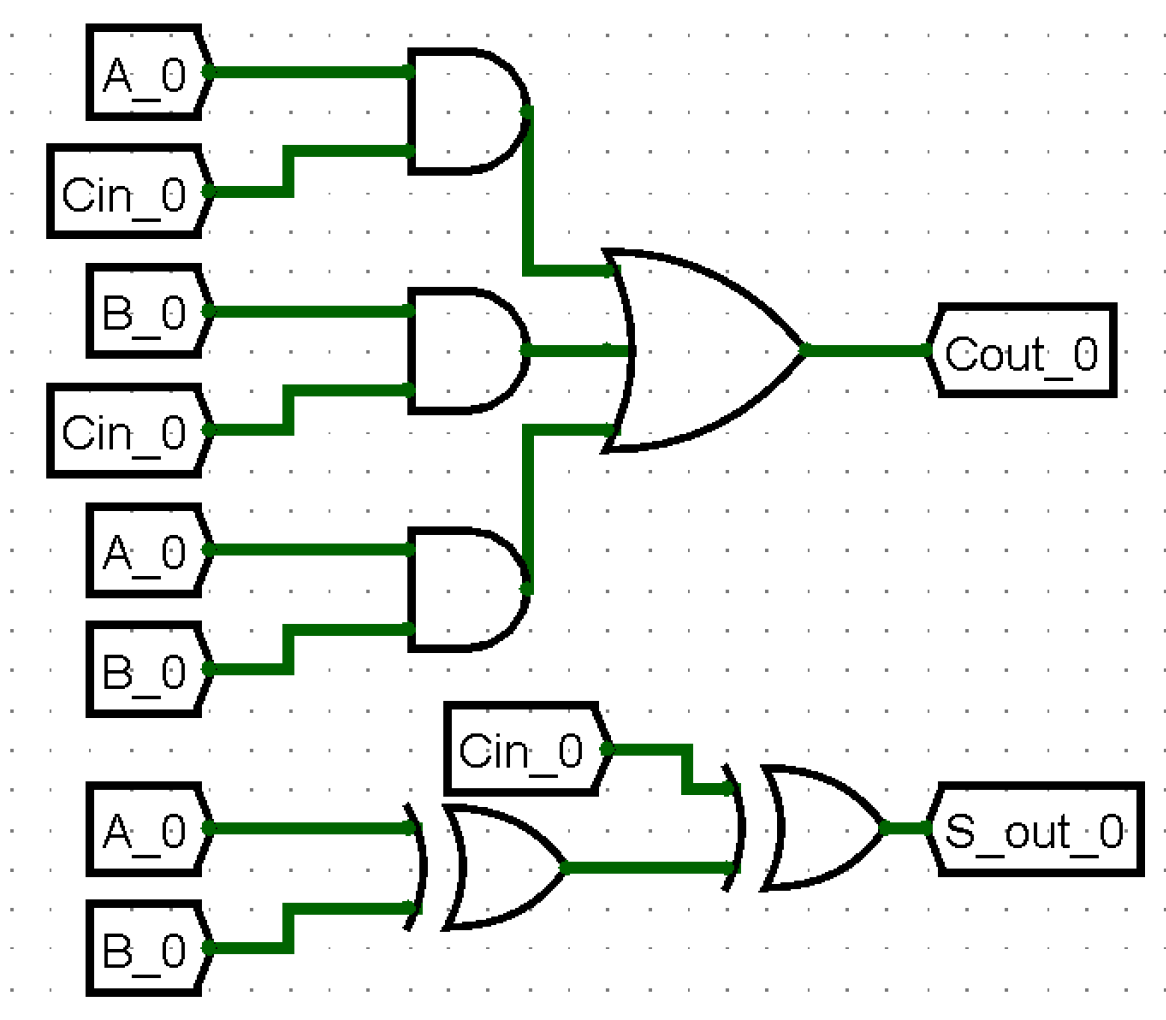
直接复用：

首先看逻辑表达式，$AB + (A + B)C_{in} = AB + (A \oplus B)C_{in}$，下证 $$ \begin{aligned} AB + (A + B)C_{in} &= AB + ((AB + A\overline{B}) + (BA + B\overline{A}))C_{in}\ &= AB(1 + C_{in}) + (A\overline{B} + \overline{A}B)C_{in}\ &= AB + (A \oplus B)C_{in}\ \end{aligned} $$ 所以也是类似半加器的，与门 + 复用异或，最后加一个或。全加器是 2 级电路（化为最小项就是 2，可以用多输入的门）。

Timing analysis

Propagation delay $T_{pd}$ = max delay from input to output，所有的输出都稳定下来

Contamination delay $T_{cd}$ = min delay from input to output，只要有一个输出发生改变了

Race Hazard 可能出现的现象：

如果 A 的输入从 0 到 1，不会有变化；但是 Ａ 的输入从 1 到 0，就会有变化。

Computational Operations & Units

Basic computational units

Multibit Carry Propagate Adders (CPA)

加法器的优化

• Ripple-carry - Slow 串行
• Carry-lookahead - Fast
• Prefix - Faster

Ripple Carry Adder (RCA)

行xing波，把各个一位全加器串起来，前一位的 $C_{out}$ 作为下一位的 $C_{in}$。

module FA (
    input x, y, cin, 
    output s, cout
);
    assign s = x ^ y ^ cin;
    assign cout = (x & y) | (x & cin) | (y & cin);
endmodule

module RCA (
    input [3:0] x, y,
    input cin,
    output [3:0] s,
    output cout,
);
    wire [4:0] c;
    assign c[0] = cin;
    FA fa0(x[0], y[0], c[0], s[0], c[1]);
    FA fa1(x[1], y[1], c[1], s[1], c[2]);
    FA fa2(x[2], y[2], c[2], s[2], c[3]);
    FA fa3(x[3], y[3], c[3], s[3], c[4]);
    assign cout = c[4];
endmodule

Carry Lookahead Adder (CLA)

如果把上面的依赖调用展开，就可以避免依赖

进一步地，如果使用下面的变量替换：

$G_i = A_iB_i$ 作为生成进位的功能

$P_i = A_i \oplus B_i$ 作为传播进位的功能

$C_{i + 1} = A_iB_i + (A_i + B_i)C_i = G_i + P_i C_i$。$S_i = P_i\oplus C_i$

这样可以有 $$ \begin{aligned} C_4 &= G_3 + P_3 G_2 + P_3 P_2 G_1 + P_3 P_2 P_1 G_0 + P_3 P_2 P_1 P_0 C_0\ &= G_3+P_3(G_2+P_2(G_1+P_1G_0)) + P_3 P_2 P_1 P_0 C_0\ &= G_{3:0}+P_{3:0}C_0 \end{aligned} $$ 所以每个 FA（全加器）都可以独立并行产生 $G_i, P_i$，然后全部提供给 CLU 来计算 $C_{i}$。之后再计算 $S_i$ 时需要 $C_{in_i}$，可以由 CLU 提供，是可以并行计算的。

CLU 是 3 级门电路，最小项的2 + G,P计算时的1 = 3

$S_i$ 是在 $C_{i}$ 基础上算的，所以是 3+1 = 4

实际使用时，不能让流入门的电路过多，所以要分成一个个 Block：例如，每4位算一次

如，定义 $$ G_{i:j} = G_i+P_i(G_{i-1}+P_{i-1}(G_{i-2}+P_{i-2}G_j))\ P_{i:j} = P_{i}P_{i-1}P_{i-2}P_{j}\ C_{i+1} = G_{i:j} + P_{i:j}C_j $$ 则有 $$ C_4 = G_{3:0} + P_{3:0}C_0\ C_8 = G_{7:4} + P_{7:4}C_4\ C_{12} = G_{11:8} + P_{11:8}C_8\ C_{16} = G_{15:12} + P_{15:12}C_{12}\ $$ 相当于每个 Block 内部是并行的，但是用串行的方式再组合起来。

Prefix Adder

由于 $C_i$ 可以看作从最低位一直到 $i$ 位的进位 Generate，所以我们定义 $C_{i} = G_{i:-1}$，然后有 $$ G_{i:j}=G_{i:k}+P_{i:k}G_{k-1:j}\ P_{i:j} = P_{i:k}P_{k-1:j} $$ 然后利用树形结构（复杂度是 $\log$ 的），用类似前缀和的方式计算？

Half Subtractor $$ D = X\oplus Y, B_{out} = \overline{X}Y $$ Full Subtractor $$ D = X\oplus Y\oplus B_{in}, B_{out} = \overline{X}Y + (\overline{X} + Y)B_{in} $$ 另一种全减器，利用补码性质：$X-Y = X + \overline{Y} + 1$，这个 $1$ 放在 $C_{in}$ 来读入进去

Fixed number operations

Adder-Subtractors 加减器

S 本身也被作为 $C_0$ 输入

Flags: Overflow Flag, Carry Flag, Zero Flag, Sign Flag

溢出 Overflow，只针对有符号的运算而言的

有符号的溢出的定义：对应了正+正=负，以及负+负=正两种情况，只要有了溢出，那结果一定不对；正数加负数一定是没有溢出的。

进位 Carry Flag 的定义：是否多了一位，代表的是比高位更高一位的数

不能依靠是否进位来判断是否溢出，比如 $(-1) + 7 = 6$，即 $1111 + 0111 = 10110$，虽然有进位，但是后 4 位结果是对的，并没有溢出。

ZF：~(|S)，所有 bits 都是 0 的时候，取反才是 1。

SF：最高位

OF：1. 符号位发生正正得负或负负得正；2. $OF = C_{n - 1} \oplus C_{n}$ $$ \begin{aligned} OF &= A_{n-1}B_{n-1}\overline{F}{n-1}+\overline{A}{n-1}\overline{B}{n-1}{F}{n-1}\ &= C_{n - 1} \oplus C_{n} \end{aligned} $$ 可以通过真值表证明。如果 $C_{n-1}=1$，$C_n=0$，意味着正正得负溢出（从 $n-2$ 位进上来一个 1，然后反而不再进位了，就相当于 $n-1$ 位（符号位）都是 0，但结果是 1）

CF：对于加法或者直接做减法，CF=1就意味着有进位/借位，CF=0意味着没有进位/借位；对于把减数取反加一再用加法的方式的减法而言，CF=1意味着没有进位，CF=0意味着有进位。

所以，对于取反加一的这种减法，对 Carry 后面的结果而言是相同的，但是会把 Carry 给取反。

实际应用时，用 $C_0=1$ 来表示进行减法运算（传入的是 $A$ 和 $\sim B$ ），用 $C_0=0$ 进行加法运算，那么就有 $CF = C_{n}\oplus C_0$。

Arithmetic logic unit (ALU)

可以实现 AND, OR, ADD 等

ALU 进行了很多运算后，有许多可以有的输出，ALU 中是逻辑门、全加器和多路选择器的结合，通过多路选择器选择到底输出哪一个 Result。

定义运算符 SLT (Set Less Than)：如果 $A<B$，输出 1；如果 $A\ge B$，输出 0。只需要在减之后的结果上，对最高位进行 0 扩展（Zero Extend）即可输出（最终输出为 0x00000001 或 0x00000000）。

Shift：逻辑左移右移、算数左移右移、循环左移右移

shamt: Shift Amount，移动几位；实现方式：多路选择器 + 连导线

Multiplication

被乘数：Multiplicand；乘数：Multiplier；部分积（竖式的中间结果）：Partial Products

由于二进制表示中，只有 0 和 1，那其实相当于被乘数左移某些位数之后，再加起来；乘数的作用是为了确定这个“某些位数”。如果乘数中每一位是 0，那对应的部分积中的那一行一定都是 0，对结果是没有影响的。

法1：由于把所有的 Partial Product 是要全加起来的，如果单独保存会占用大量内存空间，所以采用 Partial Sum 的方式，每一步都将被乘数左移一次、把乘数右移一次，然后看乘数最低位如果是 1，则把对应的被乘数加到 Partial Sum 里。

这个过程中，假设原数的位数是 $x$ bit，那部分和、被乘数以及积都需要 $2x$ bit（还需要左移），乘数需要 $x$ bit（因为只需要右移）。

缺陷：ALU和被乘数需要的位数过大，需要 $2x$；乘积在最后一步之前都不需要 $2x$；最后通过右移把乘数寄存器排空了，很多空间被浪费掉了

优化？

法2：我们只需要保证，乘数和乘积的对应最低位都相同即可；所以我们可以把乘数的最后一位和被乘数乘起来，然后把结果存在 product 的前 $x$ 位里，之后把乘数右移、product 右移，这样就大大节省了空间。

但是这里，product 还是额外占用空间了的。

法3：我们发现，乘积的后 $p$ 位是无效的，而乘数的前 $p$ 位是有效的。所以刚好可以用乘积的寄存器的后几位来存乘数，可以避免乘积寄存器的浪费。

Signed Multiplication

1. 考虑符号扩展（算术右移）
2. 最后一次的时候，乘数最高位如果是 1，那最后一次要在前x位减被乘数

Booth's Encoding

在二进制中，如果遇到连续的 1，实际上等价于把 1 的最低位对应的次方给减掉，再加上 1 的最高位的高一位对应的次方

比如，$6 = (0110)_2 = 2^3-2^1$

可以用这个来优化乘法：遇到减的就加取反加一

原理： $$ \begin{aligned} b\times \overline{a_{31}a_{30}\dots a_0} =& a_0\times b\times 2^0 + a_1\times b\times 2^1+\cdots +a_{31}\times b\times 2^{31}\ =& (0-a_0)\times b\times 2^{0} + (a_0 - a_1)\times b\times 2^1 + \cdots + (a_{30} - a_{31})\times b\times 2^{31}\&+a_{31}\times b\times 2^{32}\ \mod2^{32}\equiv& (0-a_0)\times b\times 2^{0} + (a_0 - a_1)\times b\times 2^1 + \cdots + (a_{30} - a_{31})\times b\times 2^{31} \end{aligned} $$ 用法：在最低位的最后再补一个 0，这样能增加算法通用性

还可以使用两位一组，同时判断 2 位，每次右移 2 位

If Booth’s encoding is '2': Shift multiplicand left by 1, then subtract If Booth’s encoding is '1': Subtract If Booth’s encoding is '0': Do nothing If Booth’s encoding is '1': Add If Booth’s encoding is '2': Shift multiplicand left by 1, then add

还可以直接从竖式基础上直接转换为加法器，然后使用对加法器的优化来优化。

具体算法：

像刚刚一样，最开始前 4 位表示 Product，后 4 位表示 Multiplier，然后不断右移，把新的要减/加的加到前 4 位。

Booth 算法右移的时候，无论是计算无符号还是有符号，都使用算术右移。

如，$(1000)_2\times (0100)_2$

Division

当余数>除数时，商得1

restoring division “恢复余数除法”，先减，如果发现减成负了，再恢复

需要注意：如果计算 32 位除法 ，需要多做一次，共 33 次循环

法1：除数扩展到2倍。每次循环里，首先把商左移一位，然后除数右移，然后拿被除数和它相减，如果是负则把被除数加回去然后跳过，如果是正则把商最低位设为1，（被除数已经减过除数）。

法2：只需要32次，因为第一次实际是没用的？空间上的开销可以改进，只需要把商存在被除数里，除数不变，让被除数左移

法3：不恢复余数的除法，针对法2的改进。????????? 加、Shift、减 == Shift、加

除法只能处理非符号数，对于符号数还是只能先把它取绝对值然后再加符号。

Sequential Logic Design

Introduction to sequential circuits

组合逻辑里，线不能来自两个输入，因为它不能存储状态。

时序逻辑里，可以存储状态，状态：通过当前的信息唯一确定下一个步骤的动作

双稳态电路 Bistable circuits: Latches 锁存器, Flip-flops 触发器

电平（低电平 Low 高电平 High），从低到高的那部分叫做 Rising Edge，从高到低的是 Falling Edge

时钟周期 Clock Level：信号在高和低之间的变化

Level-triggered/sensitive 电平触发/电平敏感，和电平相关的

Edge-triggered/sensitive 边缘触发/边缘敏感，发生改变的时候才会触发

脉冲触发：Pulse triggered

一般使用 Edge-triggered，因为电平维持时间一般是很长的，时时刻刻都在触发，触发器可以更好的控制触发的时间

Mealy Model: outputs = g(inputs, state)

Moore Model: outputs = h(state)，没有输入，后面的一些输入取决于之前的状态

当前状态称为 state，下一状态是 next state，则 next state = f(inputs, state)

存储单元：让状态可以保存在电路里，如通过缓冲器（如，两个反相器）这样连起来

同步时序电路 Synchronous：输出只在离散的时间发生改变，借助时钟信号实现；所有触发器的时序电路都使用同样一个时钟

异步时序电路 Asynchronous：是 clock less 的，信号是连续变化的；触发器使用不同的时钟

有限状态机 Finite state machine FSM

状态表 State Table：输入：input. current state；输出：output, next state

状态图 State Diagram

注意：变化是有时钟周期的，不是连续的

Basic sequential logic elements

双稳态电路 Bistable circuit：两个 output $Q,\overline Q$，没有输出

只要给定一个 $Q$，它会一直稳定。

SR Latch SR (Set/Reset) 锁存器

这里的变化视作连续的，直到稳定为止；有两个输出：$Q,\overline{Q}\xlongequal{\triangle}P$ $$ q = \overline{r+p}, p = \overline{s+q} $$ $S = 0, R = 0$，稳定的保存之前的状态，有两种稳态

$S = 1, R = 0$，有一种稳态 $Q = 1, P = 0$

$S = 0, R = 1$，有一种稳态 $Q = 0, P = 1$

$S = 1, R = 1$，有一种稳态 $Q = 0, P = 0$，Invalid State，如果突然再把 $S,R$ 同时置 0，会产生振荡。

只有一种稳态的合法状态时，$S$ 和 $Q$ 总是匹配的。

SR Latch with NAND Gates

输入是 $\overline{S},\overline{R}$。

可以利用它改造成控制输入的锁存器

SR Latch with Control input (Clocked SR Latch)

当时钟是 0 的时候，无论 $S,R$ 怎么变化，$Q$ 不会发生任何变化；当时钟是 1 的时候，才相当于普通锁存器。

D Latch (Data 锁存器)

输入为 $C, D$，输出 $Q=D$。$C$ 是时钟信号，为 1 才会使得输入根据 $D$ 变化。

想办法避免掉 SR Latch 中的非法状态，通过在 Clocked SR Latch 基础上对输入 $D$ 加反相器直接构造 $S,R$，保证一定是 01 或 10。

事实上只有一个输出，而且是表示不出 $S=0,R=0$ 的状态的，$S,R$ 一定相反。

锁存器可能出现问题：如果把 $\overline{Q}$ 连接到 $D$ 上，那 $Q$ 在一个时钟周期里会疯狂变化（为什么要这样连啊？？？？）。怎样让它在一个时钟周期只变化一次？

解决方法：Master-Slave flip-flop - Edge-triggered flip-flop, Pulse-triggered flip-flop

Pulse-Triggered SR Flip-flop

两个 SR 锁存器串在一起，在一整个时钟周期里完成一次。

缺陷：1's catching, 0's catching，如果发生跳变，会有问题，因为他会捕捉到跳变的那一点信号就对整个输出产生了变化

Edge-Triggered D Flip-flop

可以消除缺陷。主要就是把前面的锁存器变成 D 锁存器，后面那个可以不管。

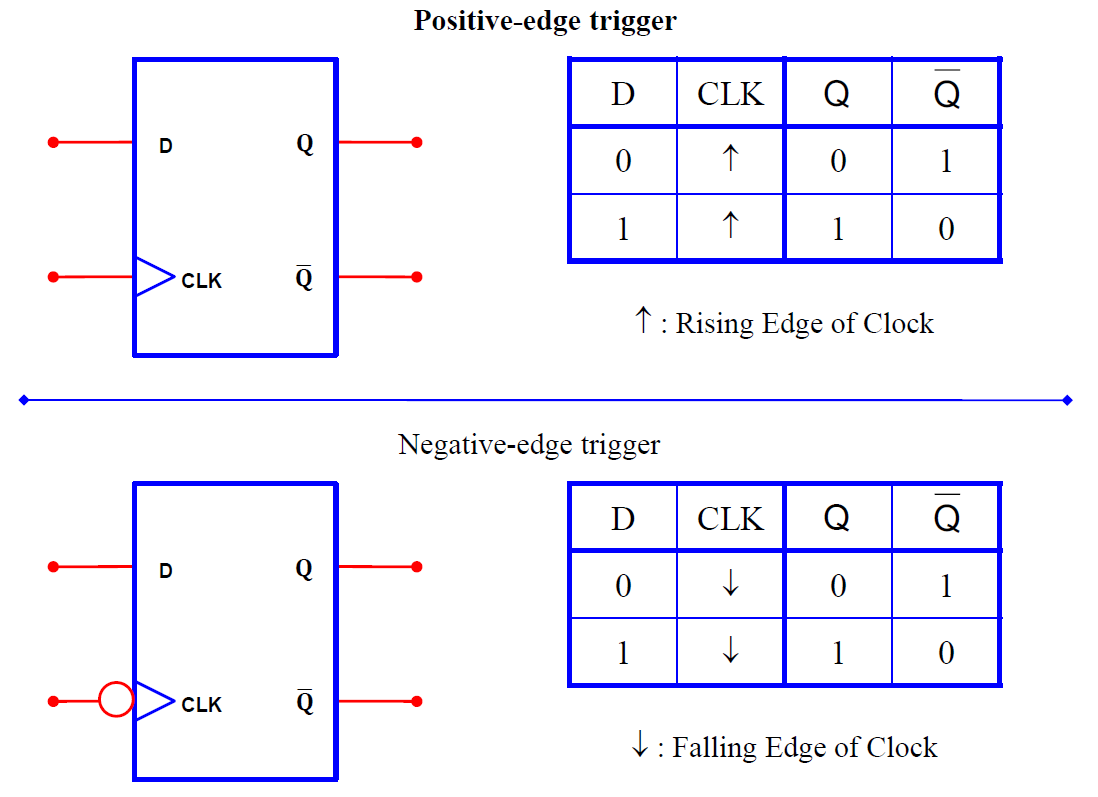
negative-edge triggered flip-flop:

positive-edge triggered flip-flop (standard flip-flop):

只捕捉时钟上升/下降时那一瞬的 $D$ 的状态，并对 $Q$ 施以影响，因为只有 Edge 时这整个触发器才是通的。

符号：

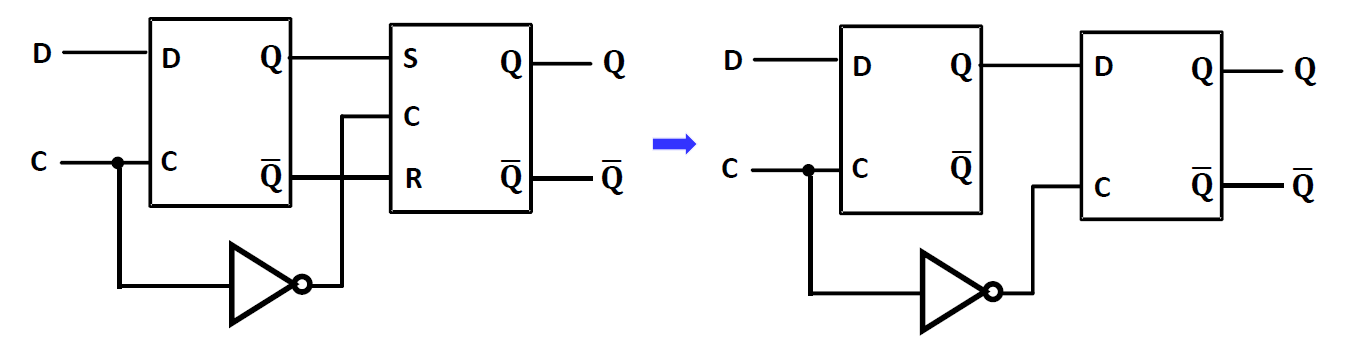
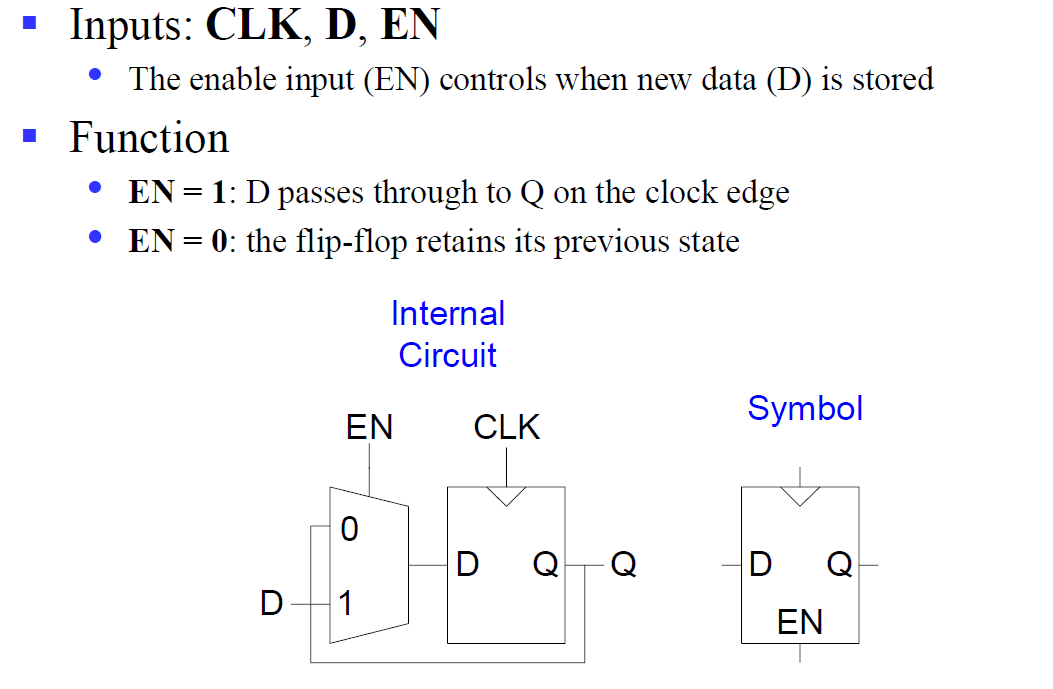
Enabled D Flip-Flop: 添加二路选择器，可以确定进入触发器的 D 是否从当前 D 更新

Resettable D Flip-Flop: 添加 Reset

左：异步；右：同步

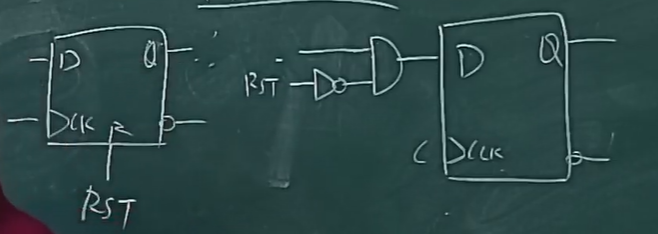
JK Flip-Flop

类似 SR 触发器，不过增加了 $J=1,K=1$ 的状态定义，是把当前状态置为相反。

同样会有 1's catching 的问题，所以可以改用 D 触发器。真值表类似 SR 触发器，只是增加了 $J=1,K=1$ 的情形。

T Flip-Flop

在 JK 触发器中，只把不改变输出（$J=0,K=0$）和将输出取反（$J=1,K=1$）两种情况拿出来，$T=0$ 时不改变状态，$T=1$ 时改变状态。

Sequential logic design

状态表、状态图

等价 Equivalent 状态

“状态” State 可以接收输入、输出。如果对于任何相同的输入，两个状态的输出都是相同的，那这两个状态称为等价的。

使用状态图、有限状态机：每条状态与状态之间的有向边上面的标注表示着个转移所对应的输入、输出。

状态图中，有 3 种形态可以化简：次态相同、次态交错、次态循环

Mealy Model: outputs = g(inputs, state)

Moore Model: outputs = h(state)，没有输入，后面的一些输入取决于之前的状态

这两种模型的状态图/表是有不同的。

Moore State 中，不需要在单向边上面写 output 标签，因为 output 只与当前的状态有关，与 input 无关，可以直接把 output 写在节点上；但是边上仍然需要写 input，这是决定往哪个状态转移

例

序列识别器：输入组合在触发点的抽象

proper sequence：需要匹配的序列的所有前缀子序列

状态表也是可以合并的

13可以合并，246也可以合并

而如果用 Moore Model 实现序列识别器，那需要多一个状态来保存最终态。Moore Model 往往会比 Mealy Model 中节点更多

状态编码方式

如 ABCD 4 种状态 4 选 1 可以用 A=00, B=01, C=10, D=11 等 24 种表达方式。

不同的编码方式可能有不同的 Cost：

因为转移过程后，需要变化的 bit 数需要尽可能相同。

确定编码之后，用类似卡诺图的方式化简。

下面这个图怎么来的？？？？？

分别对 D1, D2, Output 拎出来，用 X1, X2(input) 作为变量的不同取值

不直接用格雷码时，需要把3和4两行换顺序；用格雷码就无需。不同编码得到的结果可能不一样。

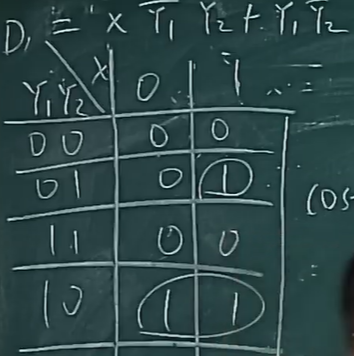
时序逻辑的 Cost = 所有的编码的组合逻辑 Cost（变量数 + Gate 数）+ Flip-flop 的 Cost

？？？？？？？？

但是要注意，如果组合逻辑部分只剩一根导线，就不用算那个 1 了。

状态设计规则：

• 下一状态完全相同的，尽可能分配到相同的编码

• 共同作为某一状态的下一可能状态的，尽可能分配到相同的编码

• 输出完全相同的，尽可能分配到相同的编码

当然大多数情况是不可以全部遵守的，而且规则只是经验性的

$Z=A(t)$ 因为 $t+1$ 实际上是下次算出来的东西，$Z$ 实际上还是这次的 $A$。

为什么会出现未使用的状态也让他转移到循环里？为了避免挂起后变为随机值的情况，使得它在一段时间之后恢复正常。

当然也可以加一个 Reset 来让它启动时强制清零。

未用状态怎么用？

代入到通过卡诺图化简其他已知状态得到的表达式，然后就可以得到未用状态时对应的下一状态和输出。

因为卡诺图化简的时候，利用了 XX，但是这可能出现过度优化（比如让未用状态也输出 1），出现把未知状态代入后与实际情况不符的情形。所以要更改卡诺图优化的表达式。

这是边缘触发！

$t_{clk}$，时钟信号周期

$t_{setup}$，时钟跳变之前，输入需要保持稳定这么久，才可以让后续电路正常捕捉到。

$t_{hold}$，时钟跳变之后，输入需要保持稳定这么久，才可以让后续电路正常捕捉到。

$t_{\mathit{ffpd}}$，时钟信号变化后，到触发器输出改变之间的延迟：在触发器里传播所需要的延迟。就是 Flip-Flop Propagation delay，触发器的 $t_{\mathit{pd}}$

$t_{comb}$，在输出下一次状态之后，会经过一段组合电路才能让这个下一状态作为流入状态

两个关系： $$ t_{\mathit{clk}}\geq t_{\mathit{ffpd}} + t_{\mathit{comb}} + t_{\mathit{setup}} $$ $$ t_{\mathit{hold}} \leq t_{\mathit{ffpd}} + t_{\mathit{comb}} $$

如果 $t_{\mathit{hold}} > t_{\mathit{ffpd}} + t_{\mathit{comb}}$，那上一次的状态仍然会残留在电路里？？？

应用：可以用不等式求最小时钟周期/最大时钟频率。

Classic sequential logic elements

Register, Counter e.g. PC (Program Counter 当前指令的下一条地址) in CPU

每个 Flip-Flop 可以看作一个 Bit 的 Register

2-bit register

Moore 型，Output 跟 Input 没关系，Input 只是确定了下一个状态

Reset 一般都是在值为 0 的时候进行 reset

时钟公用的时候的加载称为并行加载（把 Memory 中的 Load 到 Register 中，再进行运算）

门控时钟：指主时钟经过一个门电路才导入后续电路作为时钟，会出现时钟偏移，可能难以保持同步电路。

如果有额外控制的需求，可以通过控制 $D$ 而不是控制时钟来实现，在 $D$ 流入触发器之前，加入一些组合电路，让另一个 Input 可以控制这个触发器的输出。

RTL: Register Transfer Language 寄存器传输语言

if (K1 == 1)
    R2 <- R1

支持传输、算数、逻辑、移位

寄存器传输 Register Transfer Structure （狭义的传输）

多路选择器（Multiplexer-Based）、总线式（Bus-Based），三态门（Three-State，用 z 控制电路通不通）

三态总线用的更多，可以双向传输，Cost 小

移位 Shift

把几个 D Flip-Flop 串起来，利用时间信号的延迟来进行移位。

并行加载：时钟变化的时候，把时钟和一些信号取 AND 后，并行地传入各个触发器作为时钟

hold：把信号存在 D 触发器里

Counter

状态跃迁：count down, count up, or count through other fixed sequences.

可以用 counter 来记录时间/计数

Program Counter 当前指令的下一条地址

IR 寄存器 存储当前指令的内容

两种常用的寄存器：

• Ripple Counters 串行、异步、第二个触发器的时钟实际上是第一个触发器的输出再取反
• Synchronous Counters

Ripple Counter Example 图见 slides

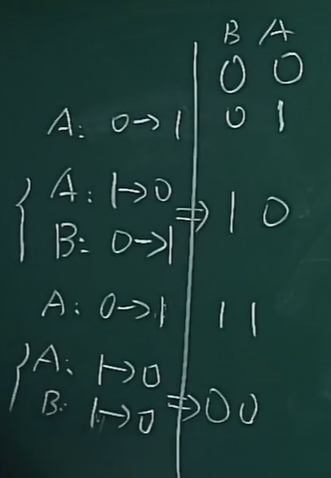
$t_{PHL}$，从上一触发器接受到时钟改变信号开始，到下一触发器收到信号所需要的时间

Worst Case: 延迟可以达到 $nt_{PHL}$

Synchronous Counters

同步 Counter，使用相同的时钟驱动

Intermenter 相当于每次自增 1 的简化版半加器组合

刚刚的仍然是串行门控，但可以优化为并行门控

Divide-by-n Counter, Modulo-n Counter

实际上可以几位几位的增，而不是一位一位的增：比如增到某个数之后，就把 1 输出，然后 counter 内又从 0 开始。

如，BCD 编码，使用4位二进制对十进制编码（有6种状态未定义，被浪费）

评论